580 -Cardinal arithmetic (6)

3. The Galvin-Hajnal theorems.

In this section I want to present two theorems of Galvin and Hajnal that greatly generalize Silver’s theorem. I focus on a “pointwise” (or everywhere) result, that gives us information beyond the pointwise theorems from last lecture, like Corollary 23. Then I state a result where the hypotheses, as in Silver’s theorem, are required to hold stationarily rather than everywhere. From this result, the full version of Silver’s result can be recovered.

Both results appear in the paper Fred Galvin, András Hajnal, Inequalities for Cardinal Powers, The Annals of Mathematics, Second Series, 101 (3), (May, 1975), 491–498, available from JSTOR, that I will follow closely. For the notion of \kappa-inaccessibility, see Definition II.2.20 from last lecture.

Theorem 1. Let \kappa,\lambda be uncountable regular cardinals, and suppose that \lambda is \kappa-inaccessible. Let (\kappa_\alpha:\alpha<\kappa) be a sequence of cardinals such that \prod_{\alpha<\beta}\kappa_\alpha<\aleph_\lambda for all \beta<\kappa. Then also \prod_{\alpha<\kappa}\kappa_\alpha<\aleph_\lambda.

The second theorem will be stated next lecture. Theorem 1 is a rather general result; here are some corollaries that illustrate its reach:

Corollary 2. Suppose that \kappa,\lambda are uncountable regular cardinals, and that \lambda is \kappa-inaccessible. Let \tau be a cardinal, and suppose that \tau^\sigma<\aleph_\lambda for all cardinals \sigma<\kappa. Then also \tau^\kappa<\aleph_\lambda.

Proof. Apply Theorem 1 with \kappa_\alpha=\tau for all \alpha<\kappa. {\sf QED}

Corollary 3. Suppose that \kappa,\lambda are uncountable regular cardinals, and that \lambda is \kappa-inaccessible. Let \tau be a cardinal of cofinality \kappa, and suppose that 2^\sigma<\aleph_\lambda for all cardinals \sigma<\tau. Then also 2^\tau<\aleph_\lambda.

Proof. Let (\tau_\alpha:\alpha<\kappa) be a sequence of cardinals smaller than \tau such that \tau=\sum_\alpha\tau_\alpha, and set \kappa_\alpha=2^{\tau_\alpha} for all \alpha<\kappa. Then \prod_{\alpha<\beta}\kappa_\alpha=2^{\sum_{\alpha<\beta}\tau_\alpha}<\aleph_\lambda for all \beta<\kappa, by assumption. By Theorem 1, \prod_{\alpha<\kappa}\kappa_\alpha=2^{\sum_\alpha\tau_\alpha}=2^\tau<\aleph_\lambda as well. {\sf QED}

Corollary 4. Let \kappa,\rho,\tau be cardinals, with \rho\ge2 and \kappa regular and uncountable. Suppose that \tau^\sigma<\aleph_{(\rho^\kappa)^+} for all cardinals \sigma<\kappa. Then also \tau^\kappa<\aleph_{(\rho^\kappa)^+}.

Proof. This follows directly from Corollary 2, since \lambda=(\rho^\kappa)^+ is regular and \kappa-inaccessible. {\sf QED}

Corollary 5. Let \rho,\tau be cardinals, with \rho\ge2 and \tau of uncountable cofinality \kappa. Suppose that 2^\sigma<\aleph_{(\rho^\kappa)^+} for all cardinals \sigma<\tau. Then also 2^\tau<\aleph_{(\rho^\kappa)^+}.

Proof. This follows directly from Corollary 3 with \lambda=(\rho^\kappa)^+. {\sf QED}

Corollary 6. Let \xi be an ordinal of uncountable cofinality, and suppose that 2^{\aleph_\alpha}<\aleph_{(|\xi|^{{\rm cf}(\xi)})^+} for all \alpha<\xi. Then also 2^{\aleph_\xi}<\aleph_{(|\xi|^{{\rm cf}(\xi)})^+}.

Proof. This follows from Corollary 5 with \rho=|\xi|, \tau=\aleph_\xi, and \kappa={\rm cf}(\xi). {\sf QED}

Corollary 7. Let \xi be an ordinal of uncountable cofinality, and suppose that \aleph_\alpha^\sigma<\aleph_{(|\xi|^{{\rm cf}(\xi)})^+} for all cardinals \sigma<{\rm cf}(\xi) and all \alpha<\xi. Then also \aleph_\xi^{{\rm cf}(\xi)}<\aleph_{(|\xi|^{{\rm cf}(\xi)})^+}.

Proof. This follows from Corollary 4: If \sigma<{\rm cf}(\xi), then \aleph_\xi^\sigma=\aleph_\xi\sup_{\alpha<\xi}\aleph_\alpha^\sigma, by Theorem II.1.10 from lecture II.2. But \xi<(|\xi|^{{\rm cf}(\xi)})^+, so both \aleph_\xi and \sup_{\alpha<\xi}\aleph_\alpha^\sigma are strictly smaller than \aleph_{(|\xi|^{{\rm cf}(\xi)})^+}. {\sf QED}

Corollary 8. If 2^{\aleph_\alpha}<\aleph_{(2^{\aleph_1})^+} for all \alpha<\omega_1, then also  2^{\aleph_{\omega_1}}<\aleph_{(2^{\aleph_1})^+}.

Proof. By Corollary 5. {\sf QED}

Corollary 9.  If \aleph_\alpha^{\aleph_0}<\aleph_{(2^{\aleph_1})^+} for all \alpha<\omega_1, then also  \aleph_{\omega_1}^{\aleph_1}<\aleph_{(2^{\aleph_1})^+}.

Proof. By Corollary 7. {\sf QED}

Notice that, as general as these results are, they do not provide us with a bound for the size of 2^\tau for \tau the first cardinal of uncountable cofinality that is a fixed point of the aleph sequence, \tau=\aleph_\tau, not even under the assumption that \tau is a strong limit cardinal. 

Now I proceed to the proof of Theorem 1.

Definition 10. Let \kappa be a cardinal and let {\mathcal A}=(A_\alpha:\alpha<\kappa) be a sequence of nonempty sets. A set {\mathcal F}\subseteq\prod_\alpha A_\alpha is an almost disjoint transversal system (a.d.t.) for {\mathcal A} iff |\{\alpha:f(\alpha)=g(\alpha)\}|<\kappa whenever f,g\in{\mathcal F}.

As in the proof of Silver’s theorem, Theorem 1 follows from an analysis of the possible sizes of a.d.t.s for a particular sequence {\mathcal A}.

Theorem 11. Let \kappa,\lambda be uncountable regular cardinals, and suppose that \lambda is \kappa-inaccessible. Let {\mathcal A}=(A_\alpha : \alpha<\kappa) be a sequence of nonempty sets such that |A_\alpha|<\aleph_\lambda for all \alpha<\kappa. Let {\mathcal F} be an a.d.t. for {\mathcal A}. Then |{\mathcal F}|<\aleph_\lambda.

Before proving Theorem 11, I show how it implies Theorem 1:

Lemma 12. Let \kappa be a cardinal and let (\kappa_\alpha:\alpha<\kappa) be a sequence of cardinals. For \alpha<\kappa let A_\alpha be the set product \prod_{\beta<\alpha}\kappa_\beta, and set {\mathcal A}=(A_\alpha:\alpha<\kappa). Then there is an a.d.t. {\mathcal F} for {\mathcal A} with |{\mathcal F}|=\prod_{\alpha<\kappa}\kappa_\alpha.

Proof of Theorem 1. Let \kappa, \lambda, and (\kappa_\alpha:\alpha<\kappa) be as in the statement of Theorem 1. Let {\mathcal A}=(A_\alpha : \alpha<\kappa) where A_\alpha=\prod_{\beta<\alpha}\kappa_\beta for all \alpha<\kappa. By Lemma 12 there is an a.d.t. {\mathcal F} for {\mathcal A} of size \prod_{\alpha<\kappa}\kappa_\alpha. By assumption, |A_\alpha|<\aleph_\lambda for all \alpha<\kappa, and it follows from Theorem 11 that |{\mathcal F}|<\aleph_\lambda as well. {\sf QED}

Proof of Lemma 12. Let \tau be the cardinal \prod_{\alpha<\kappa}\kappa_\alpha. Consider an injective enumeration (g_\eta:\eta<\tau) of the set product \prod_\alpha\kappa_\alpha. For \eta<\tau let f_\eta\in\prod_{\alpha<\kappa}A_\alpha be given by f_\eta(\alpha)=g_\eta\upharpoonright\alpha for all \alpha<\kappa. Clearly, \eta<\nu<\tau implies that \{\alpha:f_\eta(\alpha)=f_\nu(\alpha)\} is an ordinal below \kappa, namely, the least \beta such that g_\eta(\beta)\ne g_\nu(\beta). It follows that {\mathcal F}={f_\eta:\eta<\tau} is an a.d.t. for {\mathcal A}. {\sf QED}

All that remains is to show Theorem 11.

Proof. The argument is organized as an induction. For this, we need a rank on which to induct.

Definition 13. Let \kappa be a cardinal. Let <_{b,\kappa} be the partial ordering on {}^\kappa{\sf ORD} given by f<_{b,\kappa}g iff |\{\alpha<\kappa:f(\alpha)\ge g(\alpha)\}|<\kappa. (The subindex b stands for “bounded.”)

Lemma 14. If \kappa is a regular, uncountable cardinal, then <_{b,\kappa} is well-founded.

The result is fairly general. For example, instead of the ideal of bounded sets, we could have used the ideal of nonstationary sets in Definition 13 (i.e., requiring that f(\alpha)<g(\alpha) for club many values of \alpha), and Lemma 14 would still hold; all we need is a \sigma-complete ideal. Below I follow the usual convention that a \tau-complete ideal means one closed under unions of any length less that \tau.

Proof. Let {\mathcal C} be the filter of cobounded subsets of \kappa. Notice that {\mathcal C} is \kappa-complete, by regularity of \kappa. In particular, <_{b,\kappa} is indeed a partial order: If f<_{b,\kappa}g and g<_{b,\kappa}h, then f<_{b,\kappa}h because \{\alpha<\kappa: f(\alpha)<h(\alpha)\}\supseteq\{\alpha: f(\alpha)<g(\alpha)\cap\{\alpha:g(\alpha)<h(\alpha)\} contains the intersection of two sets in {\mathcal C}, so it is also in {\mathcal C}.

To prove well-foundedness, consider a <_{b,\kappa}-decreasing sequence (f_n : n<\omega), and let A_n=\{\alpha : f_{n+1}(\alpha)<f_n(\alpha)\}, so A_n\in{\mathcal C} for all n. But then A=\bigcap_n A_n\in{\mathcal C}. In particular, A\ne\emptyset. If \alpha\in\bigcap_nA_n, then \forall n\,(f_{n+1}(\alpha)<f_n(\alpha)), and (f_n(\alpha) : n<\omega) is a decreasing sequence of ordinals, contradiction. {\sf QED}

Whenever we are given a well-founded partial order on a set X, we can assign a rank (an ordinal) to the elements of X, as follows:

Definition 15. Let (X,<) be well-founded. The rank |x|_< of a set x\in X is defined by transfinite recursion as \displaystyle |x|_<=\sup\{|y|_<+1 : y<x\}.

It follows from standard arguments that, in the situation of Definition 15, |\cdot|_< : X\to{\sf ORD} is well-defined. For example, considering some x for which |x|_< is not defined (or unbounded), it follows that for some y<x, either |y|_< is not defined or it is also unbounded. This easily gives us a strictly <-decreasing sequence of members of X, contradicting that < is well-founded. It is immediate from the definition that if y<x then |y|_< < |x|_<.

Definition 16. Given a cardinal \kappa and a sequence {\mathcal B}=(B_\alpha:\alpha<\kappa) of nonempty sets, let \displaystyle T({\mathcal B})=\sup\{|{\mathcal F}|:{\mathcal F}\mbox{ is an a.d.t. for}{\mathcal B}\}.

Clearly,

  • T({\mathcal B})=T({\mathcal C}) for {\mathcal C}=(|B_\alpha|:\alpha<\kappa), i.e., T({\mathcal B}) only depends on the cardinalities of the terms of the sequence {\mathcal B}.
  • (Monotonicity). If {\mathcal B}=(B_\alpha:\alpha<\kappa) and {\mathcal C}=(C_\alpha:\alpha<\kappa) are sequences of nonempty sets with |C_\alpha|\le|B_\alpha| for all \alpha, then T({\mathcal C})\le T({\mathcal B}).

For f\in{}^\kappa\lambda let T(\aleph_f) be T({\mathcal B}) where {\mathcal B}=\aleph_f:=(\aleph_{f(\alpha)}:\alpha<\kappa). By monotonicity, Theorem 11 will follow if I can show that T(\aleph_f)<\aleph_\lambda for all f:\kappa\to\lambda, since if A_\alpha is finite for some \alpha, one can just replace it with \aleph_0. It is this reformulation that is proved by induction on the <_{b,\kappa}-rank of f.

We argue by contradiction: Assume the claim above fails, and let f be a counterexample of least <_{b,\kappa} rank. It is our goal to show that there must be another counterexample of strictly smaller rank. For this, consider the following set:

\displaystyle {\mathcal I}=\{X\subseteq\kappa : \exists g\in{}^\kappa\lambda\,\forall \alpha\in X\,(g(\alpha)<f(\alpha) \displaystyle \mbox{or }g(\alpha)=0)\mbox{ and }T(\aleph_g)\ge\aleph_\lambda\}.

All we need from Lemma 17 below is that {\mathcal I} is a nontrivial proper ideal (i.e., it is closed under finite unions, does not contain \kappa, and contains the bounded sets), but proving \kappa-completeness requires about the same amount of work.

Lemma 17. {\mathcal I} is a nontrivial \kappa-complete proper ideal on \kappa.

Proof. We prove this in four steps.

  • Clearly, {\mathcal I} is \subseteq-downward closed.
  • \kappa\notin{\mathcal I}.

Suppose \kappa\in{\mathcal I}, as witnessed by g, so T(\aleph_g)\ge\aleph_\lambda and for all \alpha<\kappa, g(\alpha)<f(\alpha) or g(\alpha)=0.

By <_{b,\kappa}-minimality of f, \{\alpha<\kappa : g(\alpha)\ge f(\alpha)\}= \{\alpha : f(\alpha)=0\} has size \kappa.

If {\mathcal F} is an a.d.t. for \aleph_g, then for h\ne j\in{\mathcal F}, we have that \{\alpha : h(\alpha)=j(\alpha)\} is bounded, so for \kappa many values of \alpha, h(\alpha)\ne j(\alpha), and they are finite! Let A be a subset of \{\alpha<\kappa: f(\alpha)=0\} of size \kappa. The number of functions from A to \aleph_0 is |{}^A\omega|=\aleph_0^\kappa, and there are at most |{\mathcal P}(\kappa)|=2^\kappa many such sets A, so the number of elements of {\mathcal F} is at most 2^\kappa\cdot\aleph_0^\kappa=2^\kappa, and |T(\aleph_g)|le2^\kappa<\lambda, contradiction.

It follows that \kappa\notin{\mathcal I}, i.e., {\mathcal I} is proper.

  • If X\subseteq\kappa is bounded, then X\in{\mathcal I}.

For X\subset\kappa bounded, let g_X:\kappa\to\lambda be given by g_X(\alpha)=f(\alpha) if \alpha\notin X, and g_X(\alpha)=0 otherwise.

I claim that g_X witnesses that X\in{\mathcal I}. Since \forall\alpha\in X\,(g(\alpha)=0), it suffices to show that T(\aleph_{g_X})\ge\aleph_\lambda.

Let {\mathcal F} be an a.d.t. for \aleph_f, and define \hat{\mathcal F} as \{\hat h : h\in{\mathcal F}\} where \hat h(\alpha)=\left\{\begin{array}{cl}h(\alpha)&\mbox{if }\alpha\notin X,\\ 0&\mbox{otherwise,}\end{array}\right. so \hat h\in\prod_{\alpha<\kappa}\aleph_{g_X(\alpha)} and h\mapsto\hat h is injective since X is bounded and h(\alpha)\ne g(\alpha) for all but boundedly many values of \alpha. Thus, \hat{\mathcal F} is an a.d.t. for \aleph_{g_X}, and it follows that T(\aleph_{g_X})\ge T(\aleph_f)\ge\lambda.

  • It remains to argue that {\mathcal I} is closed under unions of fewer than \kappa sets.

For this, let X_\beta be sets in {\mathcal I} for \beta<\gamma, where \gamma<\kappa, as witnessed by functions f_\beta, \beta<\gamma. Let X=\bigcup_{\beta<\gamma}X_\beta. Let g : \kappa\to\lambda be given by g(\alpha)=\min_{\beta<\gamma}f_\beta(\alpha) for \alpha,\kappa.

Let \mu<\aleph_\lambda. We argue that there is an a.d.t. {\mathcal F}_\mu for \aleph_g of size at least \aleph_\mu. Since this holds for all such \mu, it follows that T(\aleph_g)\ge\aleph_\lambda, and g witnesses that X\in{\mathcal I}.

To build {\mathcal F}_\mu, fix an a.d.t. {\mathcal F}^\beta for \aleph_{f_\beta} of size \mu for each \beta<\gamma, and let (f_{\beta,\delta} : \delta<\mu) be an injective enumeration of {\mathcal F}^\beta.

Partition \kappa into (possibly empty) sets Y_\beta, \beta<\gamma, such that g(\alpha)=f_\beta(\alpha) for all \alpha\in Y_\beta. Set g_\delta=\bigcup_{\beta<\gamma}f_{\beta,\delta}\upharpoonright Y_\beta for \delta<\mu, so if \alpha<\kappa and \alpha\in Y_\beta then g_\delta(\alpha)=f_{\beta,\delta}(\alpha)<\aleph_{f_\beta(\alpha)}\le \aleph_{g(\alpha)}. Let {\mathcal F}_\mu=\{g_\delta : \delta<\mu\}.

Notice that since each {\mathcal F}^\beta is an a.d.t., if \delta_1\ne\delta_2<\mu, then Z_\beta=\{\alpha\in Y_\beta : f_{\beta,\delta_1}(\alpha)=f_{\beta,\delta_2}(\alpha)\} is bounded in \kappa, so \{\alpha: g_{\delta_1}(\alpha)=g_{\delta_2}(\alpha)\}=\bigcup_{\beta<\gamma}Z_\beta is bounded in \kappa, by regularity of \kappa, so {\mathcal F}_mu is an a.d.t. for \aleph_g. {\sf QED}

Split \kappa as X_0\cup X_1\cup X_2 where X_0=\{\alpha<\kappa : f(\alpha)=0\}, X_1=\{\alpha<\kappa : f(\alpha)\mbox{ is a nonzero limit ordinal}\}, and X_2=\{\alpha<\kappa : f(\alpha)\mbox{ is a successor}\}. As argued in the proof of Lemma 17, |X_0|<\kappa, so the following holds:

Claim 18. X_0\in{\mathcal I}. \Box

Claim 19. X_1\in{\mathcal I}.

Proof. Since \lambda is regular and \kappa<\lambda, then f : \kappa\to\lambda is bounded, and we can find \rho<\lambda such that f(\alpha)\le\rho for all \alpha<\kappa. Let {\mathcal G}=\{g\in{}^\kappa\lambda : \forall\alpha\in X_1\,(g(\alpha)<f(\alpha)) and \forall \alpha\notin X_1\,(g(\alpha)=f(\alpha))\}. Then |{\mathcal G}|\le|\rho|^\kappa<\lambda.

For each \mu<\lambda fix an a.d.t. {\mathcal F}_\mu for \aleph_f with |{\mathcal F}_\mu|>\aleph_\mu. For \mu<\lambda and g\in{\mathcal G}, let {\mathcal F}_{\mu,g}={\mathcal F}_\mu\cap\prod_{\alpha<\kappa}\aleph_{g(\alpha)}, so {\mathcal F}_{\mu,g} is an a.d.t. for \aleph_g. Moreover, since f(\alpha) is a limit ordinal for all \alpha\in X_1, we have that {\mathcal F}_\mu=\bigcup_{g\in{\mathcal G}}{\mathcal F}_{\mu,g}. For \mu<\lambda sufficiently large so |\rho|^\kappa<\mu, we have that |{\mathcal G}|<\mu and therefore there must be some g_\mu\in{\mathcal G} such that |{\mathcal F}_{\mu,g_\mu}|>\aleph_\mu.

Since \lambda is regular, there must be some fixed g\in{\mathcal G} such that g=g_\mu for \lambda many ordinals \mu>|\rho|^\kappa. But then T(\aleph_g)\ge\aleph_\lambda, and g witnesses that X_1\in {\mathcal I}, as we wanted to show. {\sf QED}

It follows that X_2\notin{\mathcal I}.

For X\subseteq X_2 define g_X:\kappa\to\lambda so g_X(\alpha)=f(\alpha) if \alpha\notin X, and g_X(\alpha)+1=f(\alpha) otherwise. If X\notin {\mathcal I}, it follows that T(\aleph_{g_X})=\aleph_{\rho_X} for some \rho_X<\lambda.

Since 2^\kappa<\lambda, there is some \rho<\lambda such that 2^\kappa<\aleph_\rho and \rho_X\le\rho for all X\in{\mathcal P}(X_2)\setminus{\mathcal I}. Let {\mathcal F} be an a.d.t. for \aleph_f of size strictly larger than \aleph_{\rho+1}.

Given g\in{\mathcal F} and X\in{\mathcal P}(X_2)\setminus{\mathcal I}, let H_X(g)=\{h\in{\mathcal F} : \forall \alpha\in X\,(h(\alpha)<g(\alpha))\}. It follows that H_X(g) is an a.d.t. for (B_\alpha:\alpha<\kappa), where B_\alpha=\aleph_{f(\alpha)} if \alpha\notin X and B_\alpha=\aleph_{g(\alpha)} otherwise. By definition of g_X, we have that |B_\alpha|\le\aleph_{g_X(\alpha)} for all \alpha<\kappa, and it follows that there is an a.d.t. {\mathcal H} for \aleph_{g_X} of size |H_X(g)|. But then |H_X(g)|=|{\mathcal H}|\le T(\aleph_{g_X})=\aleph_{\rho_X}\le\aleph_\rho.

Let H(g)=\bigcup_{X\in{\mathcal P}(X_2)\setminus{\mathcal I}}H_X(g), so |H(g)|\le2^\kappa\cdot\aleph_\rho=\aleph_\rho<\aleph_{\rho+1}<|{\mathcal F}|. If {\mathcal E}\subseteq{\mathcal F} has size \aleph_{\rho+1}, there is then some g_0\in({\mathcal F}\setminus{\mathcal E})\setminus\bigcup_{g\in{\mathcal E}}H(g) and some g_1\in{\mathcal E}\setminus H(g_0).

We then have that g_0,g_1\in{\mathcal F}, g_0\ne g_1, g_0\notin H(g_1) and g_1\notin H(g_0). It follows that \{\alpha \in X_2 : g_0(\alpha)=g_1(\alpha)\}\in{\mathcal I}, since it is in fact a bounded subset of \kappa. Also, \{\alpha\in X_2 : g_0(\alpha)<g_1(\alpha)\}\in{\mathcal I}, since otherwise it is a set X such that H_X(g_1) is defined and g_0\in H_X(g_1)\subseteq H(g_1), contradiction. Similarly, \{\alpha\in X_2 : g_1(\alpha)<g_0(\alpha)\}\in{\mathcal I}.

This is a contradiction, because then X_2 is the union of three sets in {\mathcal I} and is therefore also in {\mathcal I}. {\sf QED}

This entry was posted on Tuesday, February 17th, 2009 at 2:58 pm and is filed under 580: Topics in set theory. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

14 Responses to 580 -Cardinal arithmetic (6)

  1. 580 -Cardinal arithmetic (7) « Teaching page says:
    March 4, 2009 at 12:21 am

    […] Last lecture, I covered the first theorem of the Galvin-Hajnal paper and several corollaries. Recall that the result, Theorem 3.1, states that if and are uncountable regular cardinals, and is -inaccessible, then for any sequence of cardinals such that for all […]

    Reply
  2. 580 -Cardinal arithmetic (9) « Teaching page says:
    March 7, 2009 at 9:22 am

    […] Proof: Suppose first that is -complete. If there is a -decreasing sequence let Then for all and therefore (since it is in fact an element of ) If is in this intersection, then is an -decreasing sequence of sets, contradiction. (This is just the proof of Lemma 14 in lecture II.6.) […]

    Reply
  3. 580 -Cardinal arithmetic (10) « Teaching page says:
    March 9, 2009 at 7:40 pm

    […] Zapletal has found a proof that uses a modicum of pcf theory, namely, Shelah’s result that any singular cardinal admits a scale, that is, there is an increasing sequence of regular cardinals cofinal in and a sequence of functions such that for all whenever then and whenever then for some Here, is the partial order induced by the ideal of bounded subsets of see Definition 13 in lecture II.6. […]

    Reply
  4. 580 -Cardinal arithmetic (12) « Teaching page says:
    March 13, 2009 at 12:23 am

    […] extend and improve the Galvin-Hajnal results on powers of singulars of uncountable cofinality (see lectures II.6 and II.7). His first success was an extension to cardinals of countable cofinality. For example: […]

    Reply
  5. hurburble says:
    March 13, 2010 at 1:54 am

    Hi,

    In the proof of claim 19, in the line before the last one, should it be T(aleph_g)gealeph_lambda instead of T(aleph_g)gelambda or am I being silly?

    Thanks.

    Reply
  6. andrescaicedo says:
    March 15, 2010 at 9:52 am

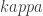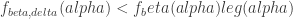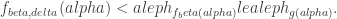    Hi! There were a few other typos as well: In the proof of Lemma 17, “partition X” should have been “partition kappa”, and f_{beta,delta}(alpha)<f_beta(alpha)le g(alpha) should have been f_{beta,delta}(alpha)<aleph_{f_beta(alpha)}lealeph_{g(alpha)}. In the paragraph above, 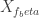X_{f_beta} should have been 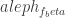aleph_{f_beta}. They are now fixed.

    Reply
  7. hurburble says:
    March 17, 2010 at 12:52 am

    Hi,

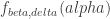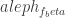    Ha yes, it is true, since the double indexed functions f_{beta,delta}(alpha) go into aleph_{f_beta(alpha)} because {mathcal F}^beta is an a.d.t for aleph_{f_beta} and that’s where the functions are by definition.

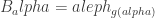    Right after the proof of claim 19, in the third paragraph of the proof of X_2notin{mathcal I}, do we need “and B_alpha=aleph_{g(alpha)} otherwise” instead of “and 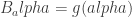B_alpha=g(alpha) otherwise”?

    R.A

    Reply
  8. Set theory seminar – Marion Scheepers: Coding strategies (IV) « Teaching blog says:
    October 12, 2010 at 3:16 pm

    […] notes, I have a proof of a general version of this result, due to Galvin and Hajnal, see Lemma 12 here; essentially, we list all functions , and then replace them with (appropriate codes for) the […]

    Reply
  9. Set theory seminar – Marion Scheepers: Coding strategies (IV) « A kind of library says:
    August 28, 2012 at 12:07 pm

    […] notes, I have a proof of a general version of this result, due to Galvin and Hajnal, see Lemma 12 here; essentially, we list all functions , and then replace them with (appropriate codes for) the […]

    Reply
  10. 580 -Cardinal arithmetic (10) « A kind of library says:
    January 20, 2013 at 9:46 am

    […] Zapletal has found a proof that uses a modicum of pcf theory, namely, Shelah’s result that any singular cardinal admits a scale, that is, there is an increasing sequence of regular cardinals cofinal in and a sequence of functions such that for all whenever then and whenever then for some Here, is the partial order induced by the ideal of bounded subsets of see Definition 13 in lecture II.6. […]

    Reply
  11. 580 -Cardinal arithmetic (12) « A kind of library says:
    January 20, 2013 at 9:53 am

    […] extend and improve the Galvin-Hajnal results on powers of singulars of uncountable cofinality (see lectures II.6 and II.7). His first success was an extension to cardinals of countable cofinality. For […]

    Reply
  12. 580 -Cardinal arithmetic (7) | A kind of library says:
    June 2, 2018 at 3:43 pm

    […] Last lecture, I covered the first theorem of the Galvin-Hajnal paper and several corollaries. Recall that the result, Theorem 3.1, states that if and are uncountable regular cardinals, and is -inaccessible, then for any sequence of cardinals such that for all […]

    Reply
  13. 580 -Cardinal arithmetic (9) | A kind of library says:
    August 5, 2020 at 5:54 pm

    […] Proof: Suppose first that is -complete. If there is a -decreasing sequence let Then for all and therefore (since it is in fact an element of ) If is in this intersection, then is an -decreasing sequence of sets, contradiction. (This is just the proof of Lemma 14 in lecture II.6.) […]

    Reply

Leave a reply to 580 -Cardinal arithmetic (10) « Teaching page Cancel reply