We verified the “surjective” version of Cantor’s theorem: If then
is not injective. A curious weakness of the standard diagonal proof is that the argument is not entirely constructive: We considered the set
and showed that there is some set
such that
.
Question. Can one define such a set ?
As a consequence of the results we will prove on well-orderings, we will be able to provide a different proof where the pair of distinct sets verifying that is not injective is definable. (Definability is an issue we will revisit a few times.)
We proved the trichotomy theorem for well-orderings, defined ordinals, and showed that is not a set (the Burali-Forti paradox).
Although I understand Cantor’s theorem and the “surjective version” well enough separately, and I even see how they are essentially saying the same thing, I don’t really understand the preamble that you were providing before presenting this version.
That is, I don’t understand why we would consider this version to be a “surjective” version of Cantor’s theorem, since it’s dealing with the nonexistence of injective functions. I also don’t understand the connection to the axiom of choice, and how the fact that a surjection A –> B corresponds (with choice) to an injection B –> A plays any part in this theorem.
My guess is that there’s a really obvious surjection implicit somewhere in the two statements, which would put everything in the right context, and I’m just missing it.
Thanks!
The “usual” version of Cantor’s result is that no injection is onto. The “surjective” version would say that no surjection
is onto. The “surjective” version would say that no surjection 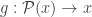 is into.
is into.
It just so happens that the argument used in the first case does not actually use that is an injection, we actually show that no such
is an injection, we actually show that no such  is onto. And, similarly, in the second case, we end up not needing to assume that
is onto. And, similarly, in the second case, we end up not needing to assume that  is a surjection. I suppose one could just as well call the
is a surjection. I suppose one could just as well call the  version the “surjective version” and the
version the “surjective version” and the  one the “injective version,” but I believe the common usage is as I have it.
one the “injective version,” but I believe the common usage is as I have it.
At the heart of both arguments is the simple diagonalization coming from wondering whether or
or  (for appropriate
(for appropriate 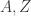 ), and it is in that sense that both arguments are more or less “the same.”
), and it is in that sense that both arguments are more or less “the same.”
As for Choice: In Tuesday we will show the fact you mention, that if there is a surjection from A onto B then there is an injection from B into A. So, with choice, both statements “A surjects onto B” and “B injects into A” are the same, and we could use either to define the relation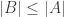 . Without choice, these statements are not equivalent, and we could have a different notion
. Without choice, these statements are not equivalent, and we could have a different notion 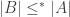 if there is a surjection from A onto B.
if there is a surjection from A onto B.
What we showed is that Cantor’s argument gives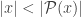 and
and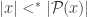 , so that x is less than
, so that x is less than  *no matter* which version of “less than” one chooses.
*no matter* which version of “less than” one chooses.
also
However, I would go further and say that the version one wants is the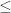 version rather than the
version rather than the  one, since the Schröder-Bernstein theorem holds for this version.
one, since the Schröder-Bernstein theorem holds for this version.
Question. Does Schröder-Bernstein hold for ?
?
(Of course, yes if we assume choice, but the question is whether it holds in ZF.)
Wait, that made perfect sense the first time I read it, but then I sat down to formalize it and realized I must be missing something. I’m pretty sure that a straight translation of your first paragraph gives…
“Usual version”: f injective => neg (f surjective)
“Surjective version”: g surjective => neg(f injective)
Um, aren’t these just contrapositives?
I fear I failed to explain myself.
We proved two different theorems. Theorem 1 says that no map is surjective. Theorem 2 says that no map
is surjective. Theorem 2 says that no map 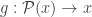 is injective.
is injective.
And we shouldn’t call them `injective’ or `surjective’ versions of Cantor’s result any longer, as this seems to be misleading.
I agree with you, the first paragraph says the same thing twice. But we actually obtained two theorems from our analysis.