Aphorismi

Hippocrates’s Aphorismi opens up with (the Greek original for) “Vīta brevis, ars longa”, or “life is short but art is long”.

Just shortly after meeting Najuma (in April 2002) I had the chance to go to the San Francisco Museum of Modern Art, where there was an art exhibit of the works of Eva Hesse. What particularly stuck with me was her use of materials that degrade easily, essentially ensuring that her works will eventually disappear. She said that “life doesn’t last, art doesn’t last, it doesn’t matter”.

It seems appropriate that I ran into Hesse’s quote again very recently. There is a curious symbolism in having Hesse’s words as bookends.

 

No durians

There clearly is a wonderful story hiding in here.

Tribus

Last year, Brittany Shelton and I coauthored a short note introducing the readers of Mathematics Magazine to Partiti, the puzzle featured in the Magazine throughout 2018. This year the Magazine will feature Tribus, a puzzle created by David Nacin.

At the invitation of Michael Jones, the magazine editor and my colleague at Mathematical Reviews, Brittany and I helped with the selection of Tribus as this year’s puzzle and wrote a very brief (one paragraph) introduction, Introducing Tribus,  which can be seen at the Magazine’s site or through my papers page (under Others).

Coloring the n-smooth numbers with n colors

Péter Pál Pach, my former master’s student Thomas A. C. Chartier and myself have just submitted our paper Coloring the -smooth numbers with colors. Meanwhile, you can access it through my papers page, or at the ArXiv.

The paper discusses the current status of a question asked by Pach around 10 years ago. I found out about the problem when Dömötör Pálvölgyi asked about it on MathOverflow. Chartier was my master’s student at Boise State and I suggested to him to work on this problem. His thesis covers the results we obtained in the process, see here. At some point I thought it seemed reasonable to publish the current partial results and contacted Pach to check whether he was indeed the originator of the problem. He mentioned he was thinking of doing the same, so we decided to exchange notes and expand what we had, and this paper is the result.

The question is the following: given , can we color the positive integers using precisely colors in such a way that for any , the numbers all receive different colors?

The problem remains open in this generality. We discuss the cases where a positive answer is known and several related problems. The results involve combinatorics, number theory and group theory. We also discuss a nice reformulation in terms of tilings that ends up being quite helpful.

Comments are welcome!

Inner-model reflection principles

Typical reflection principles in set theory are concerned with the height of the universe, or the relative height of certain stages. The resemblance between stages or between the universe itself and some of these stages is a very useful guiding principle that serves us to motivate large cardinal statements and many consequences of forcing axioms.

It is natural to wonder about similar reflection principles concerned instead with the width of the universe. In our paper Inner-model reflection principles, Neil Barton, Gunter Fuchs, Joel David Hamkins, Jonas Reitz, Ralf Schindler and I consider precisely this kind of reflection. Say that the inner-model reflection principle holds if and only if for any set , any first-order property true in the universe already holds in some proper inner model containing as an element.

We establish the consistency of the principle relative to ZFC. In fact, we build a model of the stronger ground-model reflection principle, where we further require that any such first-order reflects to a ground of , that is, an inner model with such that is a set-generic extension of . A formal advantage of this principle is that, using results in what we now call set-theoretic geology, ground-model reflection is formalizable as a first-order schema. Inner-model reflection, on the other hand, seems to genuinely require a second-order formalization. It is still open whether this is indeed the case, in our paper we explain some of the difficulties in showing this.

The paper studies the principle under large cardinals and forcing axioms, and compares it with other statements considered in recent years, such as the maximality principle or the inner model hypothesis. The most technically involved and interesting results in the paper show that inner-model reflection and even ground-model reflection hold in certain fine-structural inner models but also that this requires large cardinals, and that the large cardinal requirements differ for both principles (precisely a proper class of Woodin cardinals is needed for ground-model reflection).

Curiously, the paper started as a series of informal exchanges in response to a question on math.stackexchange.

See also here. The paper will appear in Studia Logica. Meanwhile, it can be accessed on the arXiv, or in my papers page.

Foundations of Mathematics

Foundations of Mathematics, Andrés E. Caicedo, James Cummings, Peter Koellner, and Paul B. Larson, eds., Contemporary Mathematics, vol. 690, Amer. Math. Soc., Providence, RI, 2017. DOI: 10.1090/conm/690. MR3656304. Zbl 06733965.

This book contains the proceedings of the conference in honor of Hugh Woodin’s 60th birthday, that I previously discussed on this blog (here, here, and here).

The AMS page for the volume can be found here, including the table of contents and links to the front- and endmatter (which I think are available to everybody) and links to the individual papers (which I imagine may not be).

Topological Ramsey numbers and countable ordinals

Paul Erdős and Eric Milner published in 1972 A theorem in the partition calculus, where they established that if is a countable ordinal and 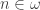, then there is a countable ordinal such that

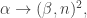
meaning that any graph whose set of vertices is either contains a clique (complete subgraph) whose set of vertices has order type or an independent set of size .

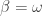The result is false if is replaced by , except for when , in which case we can take 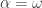as well, this is Ramsey’s theorem.

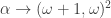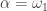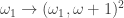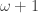The least such that is , in which case a stronger result holds, namely . In fact, more is true: the homogeneous set of order type can be taken to be a stationary subset of , and the set of type can be required to be closed, meaning that its th member is the supremum of the other members of the set. Since stationary sets contain closed subsets of any countable order type, we see that 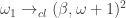holds for any countable ordinal , where the subindex cl indicates that the sets of vertices of type or 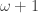are required to be closed on their supremum.

It is thus natural to wonder whether a closed version of the Erdős-Milner theorem holds. Jacob Hilton and I establish precisely this result in our paper Topological Ramsey numbers and countable ordinals.

This was a problem I had been curious about for a while, but kept not finding time to investigate. Finally I found a student at Boise State interested in working on this question for their master’s thesis, which gave me the perfect excuse to think seriously about it. I wrote a series of detailed notes for my student, who ended up leaving the program early, so I decided to continue and turn the notes into a paper. I even gave a preliminary talk on the results I had, together with some other results on the partition calculus of small countable ordinals. Hilton was a graduate student at that point, and he contacted me when he found out I was studying the problem, since this was precisely the topic of his dissertation. We decided to combine what we had, and soon we managed to extend our results and solve the full problem.

Many questions remain, as we believe the general bounds we found can be significantly improved, and it seems interesting to compute the optimal value of such that for specific values of and 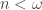. Omer Mermelstein has some striking results in this direction.

Our paper appeared in Foundations of Mathematics, the proceedings of the conference in honor of Hugh Woodin’s 60th birthday. It can also be found on the arXiv and on my papers page.

Partiti

Partiti is a puzzle created by Thinh Van Duc Lai, a Vietnamese puzzle enthusiast most of whose puzzles involve mathematics in some form. His work has been featured in The New York Times, see here. Partiti puzzles appeared on Mathematics Magazine throughout 2018.

Brittany Shelton and I coauthored a short piece introducing the puzzle to the Magazine readers at the invitation of Michael Jones, the magazine editor and a colleague at Mathematical Reviews. It is titled Of puzzles and partitions. Introducing Partiti, and can be found on the arXiv or through my papers page.

The fourteen Victoria Delfino problems and their status in the year 2019

The Cabal seminar in southern California was instrumental to the development of determinacy. The Delfino problems were suggested as a way to measure progress on this area. Fourteen problems were suggested in total through the years. Some were solved very quickly after their proposal, a few remain open.

Benedikt Löwe and I wrote a survey of their current status, cleverly titled The fourteen Victoria Delfino problems and their status in the year 2019. The cleverness has forced us to keep changing its title as its publication date kept being postponed. It is scheduled to appear in the fourth volume of the reissued Cabal volumes, which I am told is expected to finally be published this year. The volumes are being published by the Association for Symbolic Logic and Cambridge University Press as part of the Lecture Notes in Logic series.

The survey can be accessed through the Hamburger Beiträge zur Mathematik preprint server; it is paper 770 there. It can also be found through my papers page (currently under notes, and later on, once it appears, under papers).

A puzzle

October 1989 set theory workshop at the MSRI as part of its Logic Year.