This set is due February 6 at the beginning of lecture. Consult the syllabus for details on the homework policy.
1. a. Complete the proof by induction that if are integers and
, then
for all integers
.
b. This result allows us to give a nice proof of the following fact: Let be a natural number and let
be a positive integer. If the
-th root of
,
, is rational, then it is in fact an integer. (The book gives a proof of a weaker fact.) Prove this result as follows: First verify that if
and
, then
. Show that any fraction
with
integers, can be reduced so
. Assume that
is rational, say
. Then also
. Express this last fraction as a rational number in terms of
. Use that
for all
and the general remarks mentioned above, to show that
is in fact an integer.
2. Show by induction that for all integers there is a polynomial
with rational coefficients, of degree
and leading coefficient
, such that for all integers
, we have
There are many ways to prove this result. Here is one possible suggestion: Consider
.
3. Euclidean algorithm. We can compute the gcd of two integers not both zero, as follows; this method comes from Euclid and is probably the earliest recorded algorithm. Fist, we may assume that
are positive, since
, and also we may assume that
, so
. Now define a sequence
of natural numbers as follows:
,
.
- Given
, if
, then
.
- Otherwise,
, and we can use the division algorithm to find unique integers
with
such that
. Set
.
- Let
be the set of those
that are strictly positive. This set has a least element, say
. By the way the algorithm is designed, this means that
.
- Show that
, and that we can find from the algorithm, integers
such that
.
(If the description above confuses you, it may be useful to see the example in the book.)
4. Assume that the application of the algorithm, starting with positive integers , takes
steps. [For example, if
and
, the algorithm gives:
Step 1:
, so
.
Step 2:
, so
.
Step 3:
, so
, and
. Here,
]
Show that , where the numbers
are the Fibonacci numbers, see Exercises 15-22 in Chapter 1 of the book.
5. Extra credit problem. With as in the previous exercise, let
be the number of digits of
(written in base 10). Show that
[…] Homework 1, due February 6, at the beginning of lecture. Possibly related posts: (automatically generated)What Lil’ Ones Are Reading: Two Christmas Stories […]
Perhaps this is a stupid questions, but what does the notation (a,b) = 1 mean in the first problem? Is it a function that I have missed somewhere? Is it equivalent to a = b = 1, so that we are to prove that a = a^n = 1 and b = b = 1 for all integers n >= 1? I’m a little lost…
Hi. The notations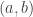 and
and  mean the same thing: The greatest common divisor of
mean the same thing: The greatest common divisor of  and
and  .
.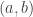 this way, but it is standard in number theory.]
this way, but it is standard in number theory.]
[I agree there is a little ambiguity in using
[…] Homework 1, due February 6, at the beginning of lecture. [This homework was not graded.] […]