502 – First order (or predicate) logic

These notes cover in some more detail what the textbook discusses in Chapter 5. Some details of my presentation will be different in irrelevant ways from the details in the book. I will be somewhat terse in terms of examples. Let me know if you feel that they are sorely needed, and I’ll amend the notes accordingly.

Predicate logic extends propositional logic in that we now allow the presence of quantifiers, and therefore we also allow the presence of statements that depend on variables. This complicates the definition of semantics, and also introduces additional complications at the syntactic level. On the other hand, this new flexibility allows us to code in straightforward ways many theories actually used in practice. Set theory is but on example of a theory that can be formalized in this context, and we will see others.

1. Syntax

These notes cover in some more detail what the textbook discusses in Chapter 5. Some details of my presentation will be different in irrelevant ways from the details in the book.

Predicate logic extends propositional logic in that we now allow the presence of quantifiers, and therefore we also allow the presence of statements that depend on variables. This complicates the definition of semantics, and also introduces additional complications at the syntactic level. On the other hand, this new flexibility allows us to code in straightforward ways many theories actually used in practice. Set theory is but on example of a theory that can be formalized in this context, and we will see others.

We begin by defining the syntax. As before, we have several options we can use. What matters is that the choice we make should allow us to prove a unique readability theorem, so we can argue by induction on (parsing sequences of) formulas, and give definitions by recursion.

The vocabulary we use to form formulas has two components, a `logical’ and a `non-logical’ one. The logical component is always the same.

Definition 1 The logical symbols of the language are {\lnot,\rightarrow} (connectives), {\forall} (quantifier), {(,)} (parentheses), {,} (comma), {=} (equality), and {v_i} for {i\in{\mathbb N}} (variables).

The non-logical part varies depending on the situation under consideration:

Definition 2 A language {{\mathcal L}} consists of a set {C} of constant symbols, a set {R} of relational symbols, and a set {F} of function symbols, together with arity functions {a_R:R\rightarrow\{1,2,\dots\}} and {a_F:F\rightarrow\{1,2,\dots\}.}

One usually refers to the elements of {{\mathcal L}} as non-logical symbols. The sets {C,R,F} are assumed disjoint, and disjoint from the set of logical symbols. They may be empty or finite, or have any infinite size; of course, we have not yet developed the theory of infinite sizes, so this extra generality won’t be too useful to us for a while. The idea is that if {a_R(S)=2,} then {S} represents a binary relation symbol, and if {a_F(f)=3,} then {f} is a ternary function symbol.

In our intended interpretation, we will fix a “universe of discourse,” and the variables will range over this universe. Before we define formulas, we describe the terms of the language. Just as the variables, the terms represent elements of the universe of discourse.

Definition 3 Given a language {{\mathcal L},} the {{\mathcal L}}-terms are finite strings of symbols from the vocabulary, defined recursively as follows:

  1. Each variable {v_i} and each constant symbol {c\in C} are terms.
  2. If {f\in F} is a function symbol of arity {j} (i.e., {a_F(f)=j}), and {t_1,\dots,t_j} are (not necessarily distinct) terms, then {f(t_1,\dots,t_j)} is a term.

In item (2), I mean the sequence

\displaystyle f{}^\frown({}^\frown t_1{}^\frown,{}^\frown t_2{}^\frown,{}^\frown\dots{}^\frown t_j{}^\frown)

One proves a unique readability lemma asserting that if the string {s} is a term, then it is either a variable, or a constant, or there is exactly one {f} of some arity {j} and exactly one sequence {t_1,\dots,t_j} of terms such that {s=f(t_1,\dots,t_j).} The argument is very similar to the argument for unique readability of formulas in propositional logic, so I will skip it. Similarly, we will need unique readability results for the definitions below. I will also skip these.

Now that we have terms we can define formulas. For this, we first define atomic formulas (that may be thought of as playing the role of propositional variables).

Definition 4 The atomic formulas of an {{\mathcal L}}-language are defined as follows:

  1. If {t_1} and {t_2} are terms, then {(t_1=t_2)} is atomic.
  2. For any {S\in R,} if {a_R(S)=j} and {t_1,\dots,t_j} are terms, then {S(t_1,\dots,t_j)} is atomic.

Now we combine the formulas as in propositional logic. We allow also for the possibility of quantifiers.

Definition 5 The formulas of an {{\mathcal L}}-language are defined recursively as follows:

  1. Atomic formulas are formulas.
  2. If {\phi,\psi} are formulas, then so are {\lnot\phi} and {(\phi\rightarrow\psi).}
  3. If {x} is a variable and {\phi} is a formula, then {\forall x\,\phi} is a formula.

Just as we did with propositional variables, we follow standard practice and (informally) omit or add parenthesis if it helps us “read” what the formulas say. Formally, we assume that only strings as described above are formulas. We also use abbreviations, such as {\phi\lor\psi} for {\lnot\phi\rightarrow\psi} and similarly for {\land,\leftrightarrow.} We also use {\exists x\,\phi} for {\lnot\forall x\,\lnot\phi.}

Additional common abbreviations and conventions described when discussing propositional logic apply here as well. Other common abbreviations are

\displaystyle \forall x_1\dots x_n\,\phi

for {\forall x_1\,\forall x_2\,\dots\,\forall x_n\,\phi,}

\displaystyle \exists x_1\dots x_n\,\phi

for {\exists x_1\,\exists x_2\,\dots\,\exists x_n\,\phi.}

The quantifier {\forall} is an inverted {A,} and read “for all.” We refer to it as the universal quantifier. The quantifier {\exists} is an inverted {E,} and read “there is” or “there exists.” We refer to it as the existential quantifier.

A common abbreviation that is sometimes useful is

\displaystyle \exists! x\,\phi

for “there is a unique {x} such that {\phi}”, formally the formula

\displaystyle \exists x\,(\phi\land \forall y\,(\phi[x/y]\rightarrow y=x)).

Here, {y} is some variable not present in {\phi,} and {\phi[x/y]} is defined by replacing each appearance of {x} in {\phi} with {y}.\footnote{This notion of {\phi[x/y]} does not coincide with the notion described in the set of notes on completeness, but it turns out to be equivalent to it since I am requiring that {y} does not appear anywhere in {\phi.}}

Other conventions typical of set theory will be introduced later.

We will typically talk about formulas without mentioning the language, with the understanding that some such language has been fixed beforehand, and the notion of formula refers to formulas in this specific language.

We need the notion of free and bound variables in order to define sentences. Intuitively, a sentence is a formula whose meaning does not depend of the particular way we `interpret’ its variables. Typically, theories consist of sentences. To proceed with the definition, one first needs to verify that given a formula {\phi} and an occurrence of a {\forall} in {\phi,} say

\displaystyle \phi\mbox{ is }s{}^\frown\forall{}^\frown t

for some (possibly empty) strings {s} and {t,} there is a unique variable {x,} a unique formula {\psi,} and a unique string {t'} such that

\displaystyle \phi\mbox{ is }s{}^\frown\forall x\,\psi{}^\frown t'.

We call the string {\forall x\,\psi} lying in between {s} and {t'} the scope of that instance of the quantifier {\forall} in {\phi.}

Definition 6 Let {x} be a variable and let {\phi} be a formula. An occurrence of {x} in {\phi} is bounded iff it lies within the scope of some quantifier. Otherwise, that occurrence of {x} in {\phi} is free.

Note that it is possible that the same variable occurs sometimes free and sometimes bounded within the same formula {\phi.} For example, if {\phi} is {\exists x\,(x=y)\land\forall y\,(y=x),} then the first two occurrences of {x} in {\phi} are bounded, but the last one is free, while the first occurrence of {y} is free, and its last two occurrences are bounded.

Definition 7 A variable {x} is free in a formula {\phi} iff {x} occurs in {\phi,} and at least one such occurrence is free. We say that {x} is bounded in {\phi} iff it occurs in {\phi,} and at least one such occurrence is bounded.

Note that in this definition, free and bounded are not complementary notions; the same variable can be free and bounded in {\phi.}

Definition 8 A sentence is a formula without free variables. A theory is a set of sentences.

In what follows, I will sometimes use the standard convention that if I write {\phi(x_1,\dots,x_k),} then it is understood that the free variables of {\phi} are among {x_1,\dots,x_k.} To avoid cumbersome notation, we allow here the possibility that some of the {x_i} are not even present in {\phi.} However, I may still write {\phi} even if there are free variables present in {\phi.}

2. Semantics

We want to define here the mathematical notion of truth. This is of course the standard notion we always use, but its formalization in this setting is somewhat cumbersome. First we introduce structures, that play the role that valuations did in propositional logic. The word is appropriate, in that structures in our sense are clearly mathematical structures in the standard sense.

Definition 9 Let {{\mathcal L}=C\cup R\cup F} be a language. An {{\mathcal L}}-structure {{\mathcal M}} is a tuple

\displaystyle {\mathcal M}=(M,C^{\mathcal M},R^{\mathcal M},F^{\mathcal M})

where:

  1. {M\ne\emptyset} is a set, called the universe of the structure {{\mathcal M}.}
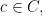
  2. {C^{\mathcal M}=\{c^{\mathcal M}\mid c\in C\},} where for each {c\in C,} {c^{\mathcal M}\in M.} We refer to {c^{\mathcal M}} as the interpretation of {c} in {{\mathcal M}.} We also say that {c^{\mathcal M}} is a constant (while {c} is but a constant symbol).
  3. {R^{\mathcal M}=\{S^{\mathcal M}\mid S\in R\},} where for each relational symbol {S\in R,} letting {j=a_R(S)} be its arity, the interpretation {S^{\mathcal M}} of {S} is a {j}-ary relation on {M,} {S^{\mathcal M}\subseteq M^j.}
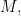
  4. {F^{\mathcal M}=\{f^{\mathcal M}\mid f\in F\},} where for each function symbol {f\in F,} the interpretation {f^{\mathcal M}} is a function in {M} of the appropriate arity, {f^{\mathcal M}:M^{a_F(f)}\rightarrow M.}

Note that, by convention, the universe of a structure is nonempty. Note also that, with a slight change in the original definitions, we could code the same information by referring solely to relational symbols. This is because, of course, we can code a function with its graph, and a constant with a function that always takes the same value. It is standard, however, to divide the collection of symbols as we have done.

The setting above (that comes from what is sometimes called “universal algebra” ) is fairly general, note that it allows us just as well to talk about groups, fields, partial orders, the natural numbers with the standard arithmetic operations, etc. The price to pay for this generality is that the definitions tend to look a bit more abstract than in each specific instance.

Now I proceed to specify how to decide whether a formula is true or false in a given structure. This requires that we first explain how to evaluate terms. For this, we need a notion of assignment (not to be confused with the notion of the same name from propositional logic).

Definition 10 Given a structure {{\mathcal M}=(M,\dots),} an assignment {{\mathfrak a}} is a function

\displaystyle {\mathfrak a}:\{v_i\mid i\in{\mathbb N}\}\rightarrow M.

How a term is interpreted is relative to the variables that are present in the term, and depends on assignments.

Definition 11 Given a term {t,} a structure {{\mathcal M}=(M,\dots),} and an assignment {{\mathfrak a},} we define the interpretation {t^{{\mathcal M},{\mathfrak a}}} of {t} in {{\mathcal M}} relative to {{\mathfrak a}} as follows:

  1. If {t} is a constant symbol {c,} then {t^{{\mathcal M},{\mathfrak a}}=c^{\mathcal M}.}
  2. If {t} is a variable {v_i,} then {t^{{\mathcal M},{\mathfrak a}}={\mathfrak a}(v_i).}
  3. If {t=f(t_1,\dots,t_j)} where {a_F(f)=j} and the {t_i} are terms, then

    \displaystyle t^{{\mathcal M},{\mathfrak a}}=f^{\mathcal M}(t_1^{{\mathcal M},{\mathfrak a}},\dots,t_j^{{\mathcal M},{\mathfrak a}}).

Note that {t^{{\mathcal M},{\mathfrak a}}\in M,} and that its value is independent of {{\mathfrak a}} if there are no variables present in {t.} More generally, if {{\mathfrak a}} and {{\mathfrak b}} are assignments, and they coincide on the variables present in {t,} then {t^{{\mathcal M},{\mathfrak a}}=t^{{\mathcal M},{\mathfrak b}}.}

Now that we know how to interpret terms, we can proceed to evaluate formulas.

Definition 12 Let {\phi} be a formula, let {{\mathcal M}=(M,\dots)} be a structure, and let {{\mathfrak a}} be an assignment. We define when {\phi} is true in {{\mathcal M}} of {{\mathfrak a},} in symbols {{\mathcal M}\models_{\mathfrak a}\phi} or {{\mathcal M}\models\phi({\mathfrak a})}, as follows:

  1. If {\phi} is {t_1=t_2} for some terms {t_1,t_2,} then {{\mathcal M}\models\phi({\mathfrak a})} iff it is the case that {t_1^{{\mathcal M},{\mathfrak a}}=t_2^{{\mathcal M},{\mathfrak a}}.}
  2. It {\phi} is {S(t_1,\dots,t_j),} where {a_R(S)=j} and {t_1,\dots,t_j} are terms, then {{\mathcal M}\models\phi({\mathfrak a})} iff {(t_1^{{\mathcal M},{\mathfrak a}},\dots,t_j^{{\mathcal M},{\mathfrak a}})\in S^{\mathcal M}.}
  3. If {{\mathcal M}\models\phi({\mathfrak a})} has been defined, then {{\mathcal M}\models\lnot\phi({\mathfrak a})} iff it is not the case that {{\mathcal M}\models\phi({\mathfrak a}),} which we can also write as {{\mathcal M}\not\models\phi({\mathfrak a}).}
  4. If {{\mathcal M}\models\phi({\mathfrak a})} and {{\mathcal M}\models\psi({\mathfrak a})} have been defined, then {{\mathcal M}\models(\phi\rightarrow\psi)({\mathfrak a})} iff either {{\mathcal M}\not\models\phi({\mathfrak a}),} or else {{\mathcal M}\models\psi({\mathfrak a}).}
  5. If {{\mathcal M}\models\phi({\mathfrak c})} has been defined for all assignments {{\mathfrak c},} then {{\mathcal M}\models\forall x\,\phi({\mathfrak a})} iff for any assignment {{\mathfrak b}} that coincides with {{\mathfrak a}} on all variables except (possibly) {x,} we have {{\mathcal M}\models\phi({\mathfrak b}).}

It may take some reflection to realize that this definition is just spelling out the “obvious” notion of truth that one actually works with. An easy induction shows that given {\phi(x_1,\dots,x_k),} a structure {{\mathcal M}=(M,\dots),} and two assignments {{\mathfrak a}} and {{\mathfrak b}} such that {{\mathfrak a}(x_i)={\mathfrak b}(x_i)} for {1\le i\le k,} then

\displaystyle {\mathcal M}\models\phi({\mathfrak a})\mbox{ iff }{\mathcal M}\models\phi({\mathfrak b}).

Because of this, we write

\displaystyle {\mathcal M}\models\phi(a_1,\dots,a_k)

for {a_1,\dots,a_k\in M} whenever {{\mathcal M}\models\phi({\mathfrak c})} for some (any) assignment {{\mathfrak c}} such that {{\mathfrak c}(x_i)=a_i} for {1\le i\le k.} Again, we should think of this as saying that the tuple {(a_1,\dots,a_k)} has property {\phi} in {{\mathcal M}.} This may help clarify the definition of {{\mathcal M}\models\forall x\,\phi({\mathfrak a}):} Given {\phi(x,\vec y),} we are saying that

\displaystyle {\mathcal M}\models\forall x\,\phi(\vec a)

iff for any {b\in M,} we have

\displaystyle {\mathcal M}\models\phi(b,\vec a);

note that the free variables of {\forall x\,\phi} are among {\vec y} regardless of whether {x} is free or not in {\phi.} Note also that if {\phi} is a sentence, then whether {{\mathcal M}\models\phi({\mathfrak a})} is actually independent of {{\mathfrak a},} and we simply write {{\mathcal M}\models\phi} in that case.

Definition 13 If {T} is a theory and {{\mathcal M}} is a structure (in the language of {T}), we say that {{\mathcal M}} is a model of {T,} in symbols {{\mathcal M}\models T,} iff {{\mathcal M}\models\phi} for all {\phi\in T.} We say that {T\models\phi} iff all models of {T} are models of {\phi.}

The notation is the usual one. For example, a group is simply a model of the theory of groups, which we could state in the language {\{1,*,{}^{-1}\}} as the set of axioms asserting the usual properties, and it is a good way of checking that one has understood the definitions to see that this is indeed the case.

Typeset using LaTeX2WP. Here is a printable version of this post.

Advertisement

This entry was posted on Monday, September 28th, 2009 at 3:29 pm and is filed under 502: Logic and set theory. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

Leave a Reply

Fill in your details below or click an icon to log in:

Gravatar
WordPress.com Logo

You are commenting using your WordPress.com account. ( Log Out /  Change )

Facebook photo

You are commenting using your Facebook account. ( Log Out /  Change )

Cancel

Connecting to %s

%d bloggers like this: