This homework is due Wednesday, February 24.
Solve the following problems from Chapter 3 of the textbook: 2, 4, 5, 7, 9, 10, 26.
In addition, solve the following problem:
Let 
![T^{-1}[S]](https://s0.wp.com/latex.php?latex=T%5E%7B-1%7D%5BS%5D&bg=ffffff&fg=333333&s=0&c=20201002)
Recall that a subset 
![\alpha\in[0,1],](https://s0.wp.com/latex.php?latex=%5Calpha%5Cin%5B0%2C1%5D%2C&bg=ffffff&fg=333333&s=0&c=20201002)
Assume that 
A kind of library
Andrés E. Caicedo
Recent Comments
Mathoverflow- Convergence of $\sum(n^3\sin^2n)^{-1}$
- Answer by Andrés E. Caicedo for Well known theorems that have not been proved
- Answer by Andrés E. Caicedo for Where is the Erdős–Rado theorem stated in Erdős and Rado's Bull AMS paper?
- Answer by Andrés E. Caicedo for The Erdős-Turán conjecture or the Erdős' conjecture?
- Relative densities
- On the division paradox
- Answer by Andrés E. Caicedo for Relative densities
- Answer by Andrés E. Caicedo for Proof theoretic ordinal
- Answer by Andrés E. Caicedo for Projection of Borel set from $R^2$ to $R^1$
- Answer by Andrés E. Caicedo for Does Turing determinacy imply full determinacy?
- Math.StackExchange
- Answer by Andrés E. Caicedo for What is the cardinality of $A \times \mathbb N$ if $\left \lvert A \right \rvert \geq \aleph_0\ $?
- Answer by Andrés E. Caicedo for Any partition of an at most countable set has a set of representatives.
- Answer by Andrés E. Caicedo for Is the class of all sets that contain the empty set as element a proper class in ZF?
- Answer by Andrés E. Caicedo for cardinal exponentiation with lower cardinal
- Answer by Andrés E. Caicedo for $\beta > 0$ and $\alpha \cdot \beta = \beta \implies \alpha ^{\omega} \leq \beta$
- Does $|X|^m\cdot n^{|X|}\le (n+m)^{|X|}$ hold without choice?
- Answer by Andrés E. Caicedo for Transfinite derivatives
- Answer by Andrés E. Caicedo for cardinals such that $\alpha < \alpha ^ \beta$
- Answer by Andrés E. Caicedo for Prove that Baire space $\omega^\omega$ is completely metrizable?
- Answer by Andrés E. Caicedo for Is it possible for a function to be smooth everywhere, analytic nowhere, yet Taylor series at any point converges in a nonzero radius?
A kind of library 
When you ask the question “Is it necessary that
is linear for this to hold, or does it suffice that 
is continuous?”, did you want simply our opinion or did you want a proof/counterexample. If a proof/counterexample is desired, can we clarify what topology we have on 
and 
. My guess is since they are finite dimensional and isomorphic to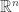 
for some 
and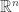 
is a metric space, we would use that.
Yes, I am thinking of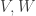
as 
and I would like a proof or a counterexample in this context.