116c- Homework 5

Homework 5

Due Wednesday, May 14 at 2:30 pm.

Update. In both parts of exercise 2, “closed” should actually be “closed in its supremum;” i.e., the subset Xof S or of {\mathbb Q} is closed in S\cap\sup(X) or {\mathbb Q}\cap\sup(X), respectively. Or, if you rather, replace the order type \alpha of X with \alpha+1. Sorry for the confusion; thanks to Fedor Manin for noticing this.

In exercise 1.(a)iii, “m<a” should be “n<b.” Thanks to Michael Conley for pointing this out.

Update. Here are sketches of the solutions of exercises 2.(a) and 3:

For 2.(a), let S\subseteq\omega_1 be a given stationary set, and argue by induction on \alpha<\omega_1 that S contains closed copies t of \alpha+1 with \min(t) arbitrarily large. (Of course, if the result of the exercise holds, this must be the case: Given any \gamma<\omega+1, notice that S\setminus(\gamma+1) is stationary, so it must contain a closed copy t of \alpha+1, and \min(t)>\gamma.)

This strengthened version holds trivially for \alpha finite or successor, by induction. So it suffices to show it for \alpha limit, assuming it holds for all smaller ordinals. Define a club C\subseteq\omega_1 with increasing enumeration \{\gamma_\beta:\beta<\omega_1\} as follows: Let (\alpha_n:n<\omega) be strictly increasing and cofinal in \alpha. Since S contains closed copies A_n of \alpha_n+1 for all n, with their minima arbitrarily large, by choosing such copies A_n with \min(A_{n+1})>\sup(A_n) and taking their union, we see that S must contain copies of \alpha, closed in their supremum, with arbitrarily large minimum element. (I am not claiming that A=\bigcup_n A_n built this way has order type \alpha. For example, if \alpha=\omega+\omega and \alpha_n=\omega+n, then A would have order type \omega^2; but for sure A\subset S is closed in its supremum and has order type at least \alpha. So a suitable initial segment of A is as wanted.)

Let \gamma_0 be the supremum of such a copy of \alpha. At limit ordinals \beta, let \gamma_\beta=\sup_{\delta<\beta}\gamma_\delta. Once \gamma_\beta is defined, find such a copy of \alpha inside S with minimum larger than \gamma_\beta, and let \gamma_{\beta+1} be its supremum.

The set C so constructed is club, so it meets S. If they meet in \gamma_0 or in a \gamma_{\beta+1}, this immediately gives us a closed copy of \alpha+1 inside S. If they meet in a \gamma_\beta with \beta limit, let (\beta_n:n<\omega) be strictly increasing and cofinal in \beta, and consider an appropriate initial segment of A=(\bigcup_n A_n)\cup{\gamma_\beta}, where A_n is a closed copy of \alpha_n+1 in S\cap[\gamma_{\beta_n},\gamma_{\beta_{n+1}}). {\sf QED}

For 3, let \kappa be regular and S\subseteq\kappa be stationary, and set T=\{\alpha\in S:{\rm cf}(\alpha)=\omega or ({\rm cf}(\alpha)>\omega and S\cap\alpha is not stationary in \alpha)\}. We claim that T is stationary. To see this, let C be an arbitrary club subset of \kappa. Then the set C' of limit points of C is also club (and a subset of C), so it meets S, since S is stationary. Let \alpha=\min(C'\cap S). Then either \alpha has cofinality \omega, so it is in T, or else it has uncountable cofinality. In that case, notice that since \alpha\in C', it is a limit of points in C, so C\cap\alpha is club in \alpha, so (C\cap\alpha)'=C'\cap\alpha is also club in \alpha. Were S\cap\alpha stationary in \alpha, it would meet C'\cap\alpha, and this would contradict the minimality of \alpha. It follows that \alpha\in T\cap C, and therefore T is stationary, as wanted.

Let now \alpha be an arbitrary point of T. If \alpha has cofinality \omega, it is the limit of an \omega-sequence of successor ordinals. Let f_\alpha be the increasing enumeration of this sequence, and notice that {\rm ran}(f_\alpha)\cap T=\emptyset, since all ordinals in T are limit ordinals. Suppose now that \alpha has uncountable cofinality, so S\cap\alpha is not stationary in \alpha. Since T\subseteq S, it follows that T\cap\alpha is not stationary either, so there is a club subset of \alpha disjoint from T, and let f_{\alpha} be the increasing enumeration of this club set.

With the sequences f_\alpha defined as above for all \alpha\in T, we now claim that there is some \xi<\kappa such that  for all \eta<\kappa, the set T_\eta=\{\alpha\in T:\xi\in{\rm dom}(f_\alpha) and f_\alpha(\xi)\ge\eta\} is stationary. The proof is by contradiction, assuming that no \xi<\kappa is as wanted.

It follows then that for all \xi<\kappa there is some \eta=\eta(\xi)<\kappa such that the set T_\eta=T_\eta^\xi as above is non-stationary. Fix a club C_\xi disjoint from it, and let C be the club C=\triangle_\xi C_\xi. Let D=C'\cap E, where E=\{\alpha<\kappa:\eta[\alpha]\subseteq\alpha\}; here, \eta:\kappa\to\kappa is the function \xi\mapsto\eta_xi. Notice that E is club, and so is D. We claim that |D\cap T|\le 1. This contradicts that T is stationary, and therefore there must be a \xi<\kappa as claimed.

Suppose then that \gamma<\alpha are points in D\cap T. Since \alpha\in D, then \alpha\in C, so \alpha\in C_\xi (hence, \alpha\notin T^\xi_{\eta_\xi}) for all \xi<\alpha. We claim that \gamma\in{\rm dom}(f_\alpha). To see this, let \xi\in\gamma\cap{\rm dom}(f_\alpha). Then (by definition of T^\xi_{\eta_\xi}), f_\alpha(\xi)<\eta_\xi. Since \gamma\in D, then \gamma\in E and,  since \xi<\gamma, then \eta_\xi<\gamma. It follows that \sup{\rm ran}(f_\alpha\upharpoonright\gamma)\le\gamma<\alpha. Since f_\alpha is cofinal in \alpha, we must necessarily have \gamma\in{\rm dom}(f_\alpha).

Since f_\alpha is continuous and \gamma is a limit ordinal (since it is in C'), it follows that f_\alpha(\gamma)= \sup_{\xi<\gamma}f_\alpha(\xi)\le \gamma. But, since f_\alpha is increasing, then also f_\alpha(\gamma)\ge \gamma. Hence, f_\alpha(\gamma)=\gamma. We have finally reached a contradiction, because \gamma\in T, but the sequence f_\alpha was chosen so its range is disjoint from T. This proves that |D\cap T|\le 1, which of course is a contradiction since T is stationary. It follows that indeed there is some \xi<\kappa such that all the sets T_\eta=\{\alpha\in T: \xi\in{\rm dom}(f_\alpha) and f_\alpha(\xi)\ge\eta\} are stationary for \eta<\kappa.

Now let f:T\to\kappa be the map f(\alpha)=\left\{\begin{array}{cl} f_\alpha(\xi)&\mbox{ if }\xi\in{\rm dom}(f_\alpha),\\ 0&\mbox{ otherwise.}\end{array}\right. Clearly, f is regressive. Also, from the definition of f, it follows that \{\alpha\in T: f(\alpha)\ge \eta\}=T_\eta for all \eta<\kappa, so f is unbounded in \kappa, since each T_\eta is in fact stationary, as we showed above. Given any \eta<\kappa, since f\upharpoonright T_\eta is regressive, there is some \gamma (necessarily, \gamma\ge\eta) such that \{\alpha\in T_\eta:f(\alpha)=\gamma\} is stationary, by Fodor’s lemma. A simple induction allows us to define a strictly increasing sequence (\gamma_\eta:\eta<\kappa) such that \{\alpha\in T_{\gamma_\eta+1}:f(\alpha)=\gamma_{\eta+1}\} is stationary for all \eta. Notice that these \kappa many subsets of T (hence, of S) so defined are all disjoint. By adding to one of them whatever (if anything) remains of S after removing all these sets, we obtain a partition of  S into \kappa many disjoint stationary subsets, as wanted. {\sf QED}

Advertisement

This entry was posted on Wednesday, May 7th, 2008 at 12:21 am and is filed under 116c: Set theory. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

One Response to 116c- Homework 5

  1. Fedor Manin says:
    May 12, 2008 at 2:07 am

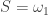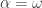    There seems to be a problem with 2(a). Say we take S=\omega_1 and \alpha=\omega. Then any subset of S of order type \alpha is bounded, but \bigcup \alpha \notin \alpha, so it is not closed in S.

    Am I misinterpreting something?

    Reply

Leave a Reply

Fill in your details below or click an icon to log in:

Gravatar
WordPress.com Logo

You are commenting using your WordPress.com account. ( Log Out /  Change )

Facebook photo

You are commenting using your Facebook account. ( Log Out /  Change )

Cancel

Connecting to %s

%d bloggers like this: