175- Partial fractions decomposition

[This post replaces the previous version from October 12, 2008. The new argument is significantly simpler than the one originally posted.]

I want to present here a Calculus II-level proof that the method of partial fractions decomposition works. I will actually show a more general result, which will greatly simplify the presentation and get rid of most problems of the somewhat awkward formulation below.

We need some notation:

$\prod_{i=1}^n a_i$ means $a_1\times a_2\times\dots\times a_n$ .
$p(x)$ , $q(x)$ , etc, denote polynomials with real coefficients.

The proof that I show below is algorithmic in nature, meaning that it provides us with a method to find the relevant constants for any given specific polynomials $p$ and $q$ . The constants we obtain are real numbers.

That the method of partial fractions decomposition works means that we can always find the relevant constants the method requires.

More precisely, I will show the following result:

Theorem. Let $q(x)$ be a non-zero polynomial with real coefficients, and let $q(x)=b\prod_{i=1}^m (x-r_i)^{l_i}\times\prod_{j=1}^k ((x+a_j)^2+p_j)^{s_j}$ be its factorization into irreducible factors, so $b\ne0$ is a constant, $m$ and $k$ are natural numbers (possibly 0), the numbers $r_1,\dots,r_m$ are all different, the numbers $l_1,\dots,l_m$ and $s_1,\dots,s_k$ are all positive integers (maybe 1), the numbers $p_1,\dots,p_k$ are all positive, and if $1\le j_1<j_2\le k$ , then either $a_{j_1}\ne a_{j_2}$ or $p_{j_1}\ne p_{j_2}$ .

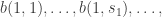
Let $n$ be the degree of $q$ . Then, for any polynomial $p$ of degree at most $n-1$ , there are unique constants $a(1,1),\dots,a(1,l_1),$ $a(2,1),\dots,a(2,l_2),\dots,$ $a(m,1),\dots,a(m,l_m),$ $b(1,1),\dots,b(1,s_1),\dots,$ $b(k,1),\dots,b(k,s_k),$ $c(1,1),\dots, c(1,s_1),\dots,$ and $c(k,1),\dots,c(k,s_k),$ (some or all of which may be 0) such that $\displaystyle \frac{p(x)}{q(x)}=\sum_{i=1}^m\sum_{h=1}^{l_i}\frac{a(i,h)}{(x-r_i)^h}+\sum_{j=1}^k\sum_{t=1}^{s_j}\frac{b(j,t)x+c(j,t)}{((x+a_j)^2+p_j)^t}.$

The proof is very simple and rests on the idea (that I explain and prove below) that the greatest common divisor of two polynomials can be expressed as a “polynomial combination” of the two. I would be glad to hear of any possible simplifications you may see.

1. Let’s begin by explaining the factorization

$q(x)=b\prod_{i=1}^m (x-r_i)^{l_i}\times\prod_{j=1}^k ((x+a_j)^2+p_j)^{s_j}.$

Suppose that $r(x)=x^2+bx+c$ is a quadratic polynomial without real roots. We say that $r$ is irreducible. We can write $r(x)= x^2+2(b/2)x+(b^2/4)+(c-b^2/4)$ or $r(x)=(x+b/2)^2+(c-b^2/4).$ The assumption that $r$ has no real roots translates into the statement that $c-b^2/4>0$ . Calling $b/2=a$ and $c-b^2/4=p$ , this shows that any irreducible quadratic polynomial can be written in the form $r(x)=(x+a)^2+p_1$ , where $p_1>0$ is some constant.

The fundamental theorem of Algebra, proved by Gauss, says that any polynomial with real coefficients can be written in a unique way as a product of linear factors and irreducible quadratic factors. This is the only nontrivial fact we are going to assume. Except for it, the proof that follows is essentially self-contained.

The factorization of $q$ as shown above comes from applying to $q$ the fundamental theorem.

2. If all the coefficients of $p$ and all the numbers $r_1,\dots, r_m,$ $a_1,\dots, a_k,$ and $p_1,\dots, p_k$ are rational, then all the constants $a(1,1),\dots, c(k,s_k)$ are rational numbers as well. This follows from the proof below.

If you know complex numbers, probably you have seen the fundamental theorem of Algebra stated in a slightly different way, namely, that any polynomial is a product of linear factors in a unique way. If we allow the use of complex numbers, so the factorization of $q$ does not require any irreducible quadratic terms, the theorem also holds. Now the coefficients of both $p$ and $q$ can be taken to be complex numbers, we can factor $q(x)=\prod_{i=1}^m (x-r_i)^{l_i}$ , and we get $\displaystyle\frac{p(x)}{q(x)}=\sum_{i=1}^m\sum_{h=1}^{l_i}\frac{a(i,h)}{(x-r_i)^h}$ , where the constants $a(1,1),\dots,a(m,l_m)$ can now be complex numbers. This also follows from the proof below.

In any case, the proof I present does not assume any knowledge of complex numbers, and no actual advantage would come from introducing them in the argument. On the other hand, I do not assume any knowledge of linear algebra either, and although the argument, as presented, does not require any linear algebra, the result seem to naturally lend itself to the language and ideas of this field; I opted for avoiding this approach to make the argument elementary.

3. We need a few preliminary results, that I present now before the proof of the theorem.

Lemma 1. If $a_0+a_1x+\dots+a_nx^n=b_0+b_1x+\dots+b_nx^n$ for all $x$ , then $a_0=b_0,$ $a_1=b_1,\dots,$ and $a_n=b_n$ .

Proof. Call $A(x)$ the expression on the left and $B(x)$ the expression on the right. Then $a_0=A(0)=B(0)=b_0$ . Taking derivatives, since $A(x)=B(x)$ , it follows that $A'(x)=B'(x)$ . Evaluating at 0, we get $a_1=A'(0)=B'(0)=b_1$ . Taking derivatives, from $A'(x)=B'(x)$ it follows that $A''(x)=B''(x)$ , so $2a_2=A''(0)=B''(0)=2b_2$ or $a_2=b_2$ . Continuing this way we get the result. ${\sf QED}$

Notice that the same argument gives that if

$a_0+a_1(x-r)+a_2(x-r)^2+\dots$ $=b_0+b_1(x-r)+b_2(x-r)^2+\dots$

for all $x$ , then again $a_0=b_0$ , $a_1=b_1$ , etc. (Now, take derivatives at $r$ rather than 0.)

Also, if $c(x)$ is an irreducible quadratic and

$(a_0+b_0 x) + (a_1+b_1 x) c(x) + (a_2+b_2 x) c(x)^2 + \dots$ $= (d_0+e_0 x) + (d_1+e_1 x) c(x) + (d_2+e_2 x) c(x)^2 + \dots$

for constants $a_0,a_1,\dots,b_0,b_1,\dots,d_0,d_1,\dots,e_0,e_1,\dots$ , then $a_0=d_0$ , $b_0=e_0$ , $a_1=d_1$ , $b_1=e_1$ , etc.

To see this, rewrite the given equality as

$(a_0-d_0)+(b_0-e_0)x = \sum_{i\ge 1}((d_i-a_i)+(e_i-b_i)x)c(x)^i.$

The left hand side is a linear polynomial and the right hand side is either 0 or a polynomial of degree at least 2, so (by lemma 1) it must be 0, and so $a_0=d_0$ and $b_0=e_0$ . Divide now by $c(x)$ and continue.

Lemma 2. Given polynomials $A(x)$ and $B(x)$ with $B(x)$ not the constant 0 polynomial, there are unique polynomials $C(x)$ and $D(x)$ with ${\rm deg}(D)<{\rm deg}(B)$ such that $A(x)=B(x)C(x)+D(x)$ .

Proof. This is just what we get from applying long division. More precisely, if we use long division, we find some polynomials $C(x)$ and $D(x)$ as wanted. Notice that if $A(x)$ and $B(x)$ have real coefficients, so do $C(x)$ and $D(x)$ , and that if $A(x)$ and $B(x)$ have rational coefficients, again so do $C(x)$ and $D(x)$ .

There is one final wrinkle, though, since we also need to show that the polynomials $C(x)$ and $D(x)$ are unique. Accordingly, assume that $C_1(x)$ and $D_1(x)$ are perhaps different polynomials such that ${\rm deg}(D_1(x))<{\rm deg}(B(x))$ and $A(x)=B(x)C_1(x)+D_1(x)$ . Then $BC+D=BC_1+D_1$ or $B\times(C-C_1)=D_1-D$ . If $C\ne C_1,$ then the left hand side has degree at least ${\rm deg}(B)$ , while the right hand side has degree at most ${\rm deg}(B)-1$ , since both $D$ and $D_1$ have degree smaller than the degree of $B$ . This is clearly impossible. [For example, it follows from Lemma 1 that this cannot happen.] We are then forced to conclude that $C=C_1$ . So the left hand side is 0, and therefore $D=D_1$ as well. ${\sf QED}$

Here is a consequence of Lemma 2 that we showed in lecture by a different method: Fix a real number $r$ . Let $A(x)$ be a polynomial of degree at most $n$ . Then we can write $A(x)=\alpha_0+\alpha_1(x-r)+\alpha_2(x-r)^2+\dots+\alpha_n(x-r)^n$ as a sum of powers of $x-r$ . To see this, notice that if we divide $A(x)$ by $(x-r)^n$ , the quotient $C(x)$ must be a constant $\alpha_n$ (since the degree of $A$ is at most $n$ ), and the remainder $D(x)$ has degree at most $n-1$ . We can then apply Lemma 2 again and divide $D(x)$ by $(x-r)^{n-1}$ to obtain a constant $\alpha_{n-1}$ as quotient and a polynomial of degree at most $n-2$ as remainder. Continuing this way we obtain the result.

The same argument gives also that if $c(x)=(x-a)^2+p_1$ for some constant $p_1>0$ is an irreducible quadratic polynomial, then we can write

$A(x)=(\alpha_0+\beta_0x)+(\alpha_1+\beta_1x)c(x)+(\alpha_2+\beta_2 x)c(x)^2+\dots$

where the sum is of course finite and the numbers $\alpha_i,\beta_i$ are constant.

Definition. The polynomial $r(x)$ is said to be a greatest common divisor of the polynomial $a(x)$ and $b(x)$ if and only if the following two conditions hold:

$r$ (evenly) divides both $a$ and $b$ .
If $s$ is a polynomial that divides both $a$ and $b$ , then $s$ divides $r$ .

There are many greatest common divisors of any two polynomials $a$ and $b$ , not both equal to 0, since if $r$ is an example, then so is $5r$ . However, except for constant multiples, there is no ambiguity. To find such $r$ , it suffices to factor both $a$ and $b$ into irreducible factors and to take $r$ to be the product of their common terms.

Lemma 3. Given any polynomials $A(x)$ and $B(x)$ with greatest common divisor $r(x)$ , there are polynomials $C(x)$ and $D(x)$ such that $A(x)C(x)+B(x)D(x)=r(x)$ . If $A$ and $B$ have rational coefficients, then $C$ , $D$ and $r$ can be chosen with rational coefficients also.

Proof. Use lemma 2 repeatedly as follows: We may assume that ${\rm deg}(A)\ge{\rm deg}(B)$ . Use lemma 2 to find $c(x)$ and $d(x)$ with ${\rm deg}(d)<{\rm deg}(b)$ , and such that

$A(x)=B(x)c(x)+d(x).$ (1)

If $d(x)=0$ , stop. Otherwise, apply lemma 2 again, this time to $B(x)$ and $d(x)$ to find $e(x)$ and $f(x)$ with ${\rm deg}(f)<{\rm deg}(d)$ , and such that

$B(x)=d(x)e(x)+f(x).$ (2)

If $f(x)=0$ , stop. Otherwise, apply lemma 2 to $d(x)$ and $f(x)$ , etc.

Notice that this process just described must stop, since the polynomials $B,d,f,\dots$ have smaller and smaller degrees. To simplify notation, assume that we find

$d(x)=f(x)g(x)+h(x),$ (3)

${\rm deg}(h)<{\rm deg}(f)$ , $h\ne0$ , and finally

$f(x)=i(x)h(x).$ (4)

Then (essentially working backwards from these equations)

$h=d-fg=d-(B-de)g=d(1+eg)-Bg=(A-Bc)(1+eg)-Bg=A[1+eg]+B[-c(1+eg)-g].$

Here, the first equality follows from (3), the second from (2), the third is a rearrangement of the previous one, the fourth follows from (1), and the last is a rearrangement of the previous one.

In general, this algorithm will give a combination of $A$ and $B$ with polynomial coefficients,

$A(x)C(x)+B(x)D(x)=r(x)$

(in this case $C(x)=1+e(x)g(x)$ , $D(x)=-c(x)(1+e(x)g(x))-g(x)$ , and $r(x)=h(x)$ ). If $G(x)$ is a greatest common divisor of $A$ and $B$ , it follows immediately that $G(x)$ divides $r(x)$ as well.

Again, working backwards we see that $h(x)$ divides $f(x)$ by (4), so $h(x)$ divides $d(x)$ , by (3), so $h(x)$ divides $B(x)$ , by (2), and also $h(x)$ divides $A(x)$ , by (1).

In general, the algorithm gives that $r(x)$ divides both $A$ and $B$ , so it divides their greatest common divisor $G(x)$ . Since $G$ also divides $r$ , the only way this is possible is for $G$ and $r$ to be multiples of each other by a constant, and so $r$ is a greatest common divisor of $A$ and $B$ . ${\sf QED}$

The above is the Euclidean algorithm and dates back to Euclid’s Elements. The same argument gives that the greatest common divisor of two natural numbers $a$ and $b$ is a linear combination $ma+nb$ of $a$ and $b$ with integer coefficients $m,n$ .

Notice, however, that there is no uniqueness here. For if $A(x)C(x)+B(x)D(x)=r(x)$ then also $A(x)[C(x)+B(x)e(x)]+B(x)[D(x)-A(x)e(x)]=r(x)$ for any polynomial $e$ .

4. We are now ready to prove the theorem.

Begin by writing $q(x)=d_1d_2\dots d_m$ where the $d_i$ have no common factors. Let $p$ be any polynomial (whose degree may be larger than the degree of $q$ ).

I claim that we can write

$\displaystyle \frac{p}{q}=a_0+\sum_{i=1}^m \frac{b_i}{d_i},$

where $a_0,b_1,\dots,b_m$ are polynomials and ${\rm deg}(b_i)<{\rm deg}(d_i)$ for all $i.$

The argument to follow is an example of mathematical induction. We argue that the claim is true if $m=1$ , and then show how knowing the truth of the claim for $m-1$ factors $d_i$ gives also the truth for $m$ factors. Combining these two bits of information, it follows that the claim is true, no matter how many factors $q$ has.

For $m=1$ the result follows from lemma 2: We have $q=d_1$ and we can write $p=a_0d_1+b_0$ for some polynomials $a_0$ and $b_1$ with ${\rm deg}(b_1)<{\rm deg}(d_1)$ , so

$\displaystyle \frac{p}{q}=a_0+\frac{b_0}{d_1},$

which is precisely what the claim says when $m=1$ .

Assume the result is true when $q$ is a product of $m-1$ polynomials with (pairwise) no common factors, and assume $q=d_1d_2\dots d_m$ where the $d_i$ have no common factors.

Call $d=d_2\dots d_m$ , so $d_1$ and $d$ have no common factors either. It follows from lemma 3 that we can find polynomials $e$ and $f$ such that

$d_1e+d_2f=1.$

Then

$\displaystyle \frac{p}{q}=\frac{p1}q=\frac{p(d_1e+df)}{d_1d}=\frac{pf}{d_1}+\frac{pe}d.$

Applying the case $m=1$ of the claim, we find polynomials $c_0$ and $b_1$ with ${\rm deg}(b_1)<{\rm deg}(d_1)$ such that

$\displaystyle \frac{pf}{d_1}=c_0+\frac{b_1}{d_1}.$

Applying the claim with $d_2\dots d_m$ in place of $q$ and $pe$ in place of $p$ , since we are assuming that the result follows for products of $m-1$ many factors, swe have that there are polynomials $k_0$ and $b_2,\dots,b_m$ with ${\rm deg}(b_i)<{\rm deg}(d_i)$ such that

$\displaystyle \frac{pe}{d}=k_0+\sum_{i=2}^m\frac{b_i}{d_i}.$

Combining these two facts and setting $a_0=c_0+k_0$ , we have the claim.

5. In the above, we could have $d_i=(x-r)^l$ or $d_i=((x+a)^2+p_1)^{s}$ , in which case we can use the observation following lemma 2 above, to continue further: Say $d_i=(x-r)^l$ . As explained after lemma 2, we can write $b_i=\alpha_0+\alpha_1(x_r)+\dots+\alpha_{l-1}(x-r)^{l-1}$ for some constants $\alpha_0,\dots,\alpha_{l-1}$ , the sum has only $l-1$ many factors since ${\rm deg}(b_i)<{\rm deg}(d_i)=l.$

But then

$\displaystyle\frac{b_i}{d_i}=\sum_{t=0}^{l-1}\frac{\alpha_t}{(x-r)^{l-t}}.$

We obtain a similar expansion if $d_i$ is a power of an irreducible quadratic, but now instead of the constant coefficients $\alpha_t$ we obtain linear factors $\alpha_t+\beta_t x$ .

Doing this for each factor $d_i$ gives the theorem. (We still need to see that if ${\rm deg}(p)<{\rm deg}(q)$ then what we called $a_0$ above must in fact be 0, and that we have uniqueness.)

6. We are almost done. The only bit of the theorem that remains to be checked is the claim that the constants we find are unique, meaning that there is only one possible decomposition of the sort claimed in the theorem.

We actually show that there is uniqueness in the expressions found in item 4. For this, suppose we have

$\displaystyle a_0+\sum_{i=1}^m\frac{b_i}{d_i}=c_0+\sum_{i=1}^m\frac{e_i}{d_i}$

for some polynomials $a_0,b_1,\dots,b_m,c_0,e_1,\dots,e_m$ with ${\rm deg}(b_i),{\rm deg}(e_i)<{\rm deg}(d_i)$ .

Then

$\displaystyle a_0-c_0=\sum_{i=1}^m\frac{e_i-b_i}{d_i}=\frac{r}{q}$

for some polynomial $r$ that necessarily has degree less than the degree of $q$ . But the only way this is possible is if $a_0=c_0$ , so $r=0$ . (This also shows that $a_0=0$ if ${\rm deg}(p)<{\rm deg}(q)$ .)

Now argue by induction on $m$ . The case $m=1$ is trivial, since then we have $b_1/d_1=e_1/d_1$ , so $b_1=e_1$ .

Assuming the result for $m-1$ , now consider $q$ with $m$ many factors, so we can write

$\displaystyle\frac{b_1-e_1}{d_1}=\sum_{i=2}^m\frac{e_i-b_i}{d_i}=\frac{Q}{d_2\dots d_m}$

for some polynomial $Q$ of smaller degree than $d_2\dots d_m$ . Since $d_1$ and $d_2\dots d_m$ have no common factors and

$\displaystyle b_1-e_1=\frac{Q}{d_2\dots d_m}d_1,$

we must have that $d_2\dots d_m$ actually divides $Q$ . Since $Q$ is of smaller degree, the only possibility is that $Q=0$ , so $b_1=e_1$ . But then we also have

$\displaystyle\sum_{i=2}^m\frac{b_i}{d_i}=\sum_{i=2}^m\frac{e_i}{d_i},$

and the inductive assumption gives us that $b_2=e_2,\dots,b_m=e_m$ .

7. Finally, using lemma 1 (or rather, lemma 1 and the observations following it), we complete the proof of uniqueness, since if

$\displaystyle \frac{p(x)}{q(x)}=\sum_{i=1}^m\sum_{h=1}^{l_i}\frac{a(i,h)}{(x-r_i)^h}+\sum_{j=1}^k\sum_{t=1}^{s_j}\frac{b(j,t)x+c(j,t)}{((x+a_j)^2+p_j)^t}$

equals a similar expression with possibly different coefficients, the argument of item 6 gives that we must have that the expressions with powers of $(x-r_i)$ are the same, and then lemma 1 gives that their coefficients are the same, and the same follows for the expressions with powers of a fixed irreducible quadratic.

And with this, we are done. ${\sf QED}$

Please let me know of typos, and whether there are parts of the argument above that are not explained clearly or that you are not sure you understand completely; it may be a good idea to first work through the argument with a few examples, since this may help clarify what it is that we are doing.

To conclude, let me point out that even though the proof above provides an algorithm for finding the required constants, I believe (but haven’t checked that) the methods discussed in class are somewhat faster. It turns out that the argument above dates back to Hermite. In any case, the point of the argument above is not so much to give yet another method for finding the constants of the partial fractions decomposition, as it is to provide us with evidence that, whichever method we use, we can be assured that it will be successful, and we will be able to find some such decomposition.

Also, notice the argument becomes very simple by just arguing about an arbitrary `decomposition’ of $q$ into pieces with no common factors, so the result one is after becomes a very particular case. And the method is quite general, for example, it works if $p$ and $q$ are numbers and we measure with absolute value rather than degree, so we get: If $q=p_1^{n_1}p_2^{n_2}\dots$ is the factorization of $q>1$ into prime numbers, and $m$ is an integer, then there is a unique way of writing

$\displaystyle\frac mq=n+\sum_i\frac{m_i}{p_i^{n_i}}$

where $n,m_1,m_2,\dots$ are integers, $nq\le m$ , and $|m_i|<p_i^{n_i}$ ; moreover, there is a unique way of writing

$\displaystyle\frac{a}{p^n}=\sum_{i=1}^n\frac{a_i}{p^i}$

for $a$ an integer with $|a|<p^n$ as a sum of fractions with $|a_i|<p$ . This is usually called the $p$ -adic decomposition of $a/p^n$ .

This entry was posted on Tuesday, November 18th, 2008 at 5:51 pm and is filed under 175: Calculus II. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

4 Responses to 175- Partial fractions decomposition

Partitioning numbers « Teaching page says:

November 18, 2008 at 5:59 pm

[…] the method of partial fractions decomposition, we see that Notice that , […]

Reply
175, 275 -Suggestions for next week. « Teaching page says:

November 18, 2008 at 6:01 pm

[…] a look at Talman’s paper; see here); but it won’t include the proof that the method of partial fractions decomposition works. For 275, you may want to review the polar expression of the Laplacian and how to derive it. […]

Reply
andrescaicedo says:

August 24, 2014 at 4:37 pm

[Comment by Chingyun Hsu on Jun 18, 2014 @ 7:20, at the old site. I’ve corrected the typo.]

Hi! I think there might be a typo here:

Assuming the result for $m-1$ , now consider $q$ with $m$ many factors, so we can write

$\displaystyle\frac{b-1-e_1}{d_1}=\sum_{i=2}^m\frac{e_i-b_i}{d_i}=\frac{Q}{d_2\dots d_m}$

It should be

$\displaystyle\frac{b_1-e_1}{d_1}=\sum_{i=2}^m\frac{e_i-b_i}{d_i}=\frac{Q}{d_2\dots d_m}$

Reply
175, 275 -Suggestions for next week. | A kind of library says:

February 19, 2019 at 10:54 am

[…] a look at Talman’s paper; see here); but it won’t include the proof that the method of partial fractions decomposition works. For 275, you may want to review the polar expression of the Laplacian and how to derive it. […]

Reply

	ปั่นสล็อต on 414/514 The theorems of Rieman…
	Richard Kimberly Hec… on Woodin’s proof of the se…
	Is there a Borel-mea… on 414/514 Examples of Baire clas…
	Simple bijectiveness… on 580 -Some choiceless results…
	Schur’s theore… on 580 -III. Partition calcu…
	Uncountable linearly… on 403/503 – Homework …
	What is a non-constr… on On strong measure zero se…
	function from Nmathb… on Hindsight
	Cauchy Schwarz Inequ… on 275 -Positive polynomials
	What is a Cantor-sty… on 580 -Some choiceless results…
	Question about Gener… on 580 -Some choiceless results…
	Set has Measure Zero… on On strong measure zero se…
	Non-measurable subse… on 580 -Cardinal arithmetic …
	hmeng1 on 414/514 The theorems of Rieman…
	580 -Cardinal arithm… on 580 -Cardinal arithmetic …

M	T	W	T	F	S	S
					1	2
3	4	5	6	7	8	9
10	11	12	13	14	15	16
17	18	19	20	21	22	23
24	25	26	27	28	29	30

A kind of library