1. Colorings of pairs. I
There are several possible ways in which one can try to generalize Ramsey’s theorem to larger cardinalities. We will discuss some of these generalizations in upcoming lectures. For now, let’s highlight some obstacles.
Theorem 1 (
-Kakutani)
In fact,

Proof: Let Let
be given by
Then, if are distinct, it is impossible that
Proof: With as above, let
be given as follows: Let
be a well-ordering of
in order type
Let
be the lexicographic ordering on
Set
Lemma 3 There is no
-increasing or decreasing
-sequence of elements of
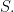
Proof: Let be a counterexample. Let
be least such that
has size
and let
be such that if
then
To simplify notation, we will identify
and
For
let
be such that
but
By regularity of
there is
such that
for
many
But if and
then
iff
so
It follows that
has size
contradicting the minimality of
The lemma implies the result: If has size
and is
-homogeneous, then
contradicts Lemma 3.
Now I want to present some significant strengthenings of the results above. The results from last lecture exploit the fact that a great deal of coding can be carried out with infinitely many coordinates. Perhaps surprisingly, strong anti-Ramsey results are possible, even if we restrict ourselves to colorings of pairs.
Recall our convention that if for some subset
of a linearly ordered set, then
proved the following theorem in 1987. This is one of the gems of modern combinatorial set theory. Previous versions of this result were known to
Hajnal and Rado in the presence of
The argument below is due to Velleman, from 1990; thanks to Assaf Rinot for pointing me to this argument.
Theorem 4 (
)
i.e., there is a function
such that whenever
then
![{f''[X]^2=\omega_1.}](https://s0.wp.com/latex.php?latex=%7Bf%27%27%5BX%5D%5E2%3D%5Comega_1.%7D&bg=ffffff&fg=000000&s=0&c=20201002)
Proof: As in the proof of Theorem 4 from last lecture, it is enough to find a function such that whenever
then
contains a club. In effect, let
be such that
is stationary for all
and consider
If
then
for all
so
To define begin with an injective sequence
of functions
Also, for each
fix an injection
For countable ordinals let
For let
and set
To see that is as wanted, fix an uncountable
For
let
If is countable, let
Otherwise, let
Finally, set
so is club. Now we show that
To see this, pick and
with
We will find an
such that
and
Let
and so
or
Since
and
we have that
so
is uncountable, and
For in
let
and
Since
and, by the definition of
but
so
Since is uncountable, there is an uncountable
an
and an
such that for all
(
)
and
so
and it follows that
Then
is uncountable and, since
Note that
Let
Note that is finite, since
is injective. We can then find an
with
Note that
Since then
Since
and
then
Since
and
then
Finally, if then, since
we must have
It follows that
so
This shows that
Since
was arbitrary, it follows that
and we are done.
The result also holds for many larger cardinals. For example, we have the following generalization obtained independently by Shelah and The proof below is Shelah’s.
Theorem 5 (Shelah,
) Suppose
is an uncountable regular cardinal and there is some nonreflecting stationary subset of
Then
![{\lambda\not\rightarrow[\lambda]^2_\lambda.}](https://s0.wp.com/latex.php?latex=%7B%5Clambda%5Cnot%5Crightarrow%5B%5Clambda%5D%5E2_%5Clambda.%7D&bg=ffffff&fg=000000&s=0&c=20201002)
Proof: We use the method of walks.
Fix stationary and nonreflecting; we may assume that all the ordinals in
are limit ordinals. For each nonzero
choose
so that:
- If
is limit,
is club in
and disjoint from
and any point of
is a successor ordinal.
Fix a partition of
into stationary sets.
Given in
define
by induction on
- If
is defined and strictly larger than
let
and
- Let
be the least
such that
At this point, the construction stops.
We can think of the sequence of as describing a walk from
down to
through the ladders
Note that
is well-defined, since the
form a decreasing sequence of ordinals.
Note that if are in
and
then
For
we have
and equality occurs only if
Suppose are in
Let
Set
Then and, if
then
and
for all
and
Now define as follows: Given
in
let
be largest such that, letting
for all
for all
and
if such an exists, and in that case let
be the unique
such that
Otherwise let
(The strange looking condition 2 will be used at the end of the argument. For now, notice that if does not satisfy conditions 1 and 2, then no larger
can satisfy them either.)
Let now and
be given. We need
in
with
Consider the model where
holds iff
Let
be a continuous increasing sequence of elementary substructures of
with
and
for all
Note that there is a club of ordinals such that
This is because both
and
are filtrations of
Definition 6 A filtration of
is a strictly increasing continuous sequence
with union
such that
for all
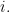
(The above definition is somewhat more restrictive than the general notion of filtration one finds in algebra.) Suppose and
are filtrations of
By regularity of
given any
we can find
such that
and similarly there is some
such that
By an obvious back-and-forth argument we can find a club of ordinals
such that
In particular, for club many
We can then find a limit ordinal
such that
Choose
so
and
is defined and larger than
Let We claim that
Note that if then
and therefore
since
is limit.
If then
Since
then
is a successor ordinal, and must therefore be
Hence
This is the only place in the argument where we use the assumption that
is nonreflecting.
Thus for all
Therefore
as claimed.
Let be the first-order formula in the language of
with parameters
for all
asserting that, letting
and
for all
we have that:
is limit,
for all
and
(That there is such a formula takes but a moment’s thought and is best argued by induction on The strange looking condition 4 is the counterpart of condition 2 in the definition of
and will be used towards the end of the argument.)
Note all the parameters in belong to
and
since
Recall that and
Let
Then
so, by elementarity, the same holds in Since
was arbitrary,
Now let Then
By elementarity, the same holds in and, since
was arbitrary, then
Therefore there are in
such that
and
For all since
we have that
and
In particular, for all
and
and therefore
We claim that
To see this, notice that if then:
for all
since
and
Here,
denotes
for all
This means that satisfies the requirements of
in the definition of
On the other hand, and, since
it is larger than
But then no satisfies the requirements of
in the definition of
To see this, note that
If then
for all in particular for
However, we must also have so
This means that in the definition of
and
Since
we are done.
Corollary 7 If
is regular,
![{\lambda^+\not\rightarrow[\lambda^+]^2_{\lambda^+}.}](https://s0.wp.com/latex.php?latex=%7B%5Clambda%5E%2B%5Cnot%5Crightarrow%5B%5Clambda%5E%2B%5D%5E2_%7B%5Clambda%5E%2B%7D.%7D&bg=ffffff&fg=000000&s=0&c=20201002)
Proof: The set is stationary and nonreflecting. This is because
consists of ordinals of cofinality
for any
If
is a club set of minimal order type, such that every ordinal in
is a successor, then no ordinal in
has cofinality
and therefore
avoids
This implies that for all nonzero
The situation for is different, and we turn to it before moving to larger cardinals.
The argument of Theorem 5 makes use of (basic) ideas from mathematical logic. This is a very useful tool in combinatorial set theory, and more substantial applications will be encountered in future lectures.
2. Canonical partitions
Definition 8 Let
let
be a set, and let
A function
is
-canonical on
iff whenever
and
are subsets of
then
iff
for all
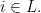
(Compare with the discussion of canonical relations in of lecture III.1.)
Here are some examples; suppose that and that
is
-canonical on
Then:
iff
is constant on
iff
is injective on
iff
is (strictly) min-homogeneous, i.e., whenever
then
iff
iff
is (strictly) end-homogeneous, i.e.,
iff
iff
is (strictly) max-homogeneous, i.e.,
iff
(The nonstrict versions are obtained by replacing equivalence with implication: is min-homogeneous iff
whenever
etc.)
Theorem 9 (
-Rado) If
then there is some
and an
such that
is
-canonical on

Note that if is finite, then necessarily
so this generalizes Ramsey’s theorem.
Theorem 10 For all
and all
there is an
-canonical partition of
![{[\omega]^r.}](https://s0.wp.com/latex.php?latex=%7B%5B%5Comega%5D%5Er.%7D&bg=ffffff&fg=000000&s=0&c=20201002)
Proof: The obvious attempt is to define by
where if and
then
means that
Clearly, if then
Conversely, suppose Let
Then
so
Hence,
Conversely,
Recall now the ultrafilter proof of Ramsey’s theorem from of lecture III.1. We showed there that if
is a nonprincipal ultrafilter over
and
for some finite
then there is some infinite set
and a color
such that
and
Here,
Definition 11 An ultrafilter
over
is Ramsey iff it is nonprincipal and for all

is generated by the sets
for

Whether there are Ramsey ultrafilters is independent of and follows from
It follows from the definition and the argument in of lecture III.1 that a nonprincipal ultrafilter
over
is Ramsey iff for any
and any finite coloring of
there is some
such that
is monochromatic.
For we have a “Ramsey-ultrafilter” version of Theorem 9:
Homework problem 14. Let be a nonprincipal ultrafilter over
Show that
is Ramsey iff for any
there is some
such that
is 1-1 or constant.
Now we proceed to the proof of the canonization Theorem 9:
Proof: Let be given. For
let
be the set of all tuples
where
and
(Note that, against convention, we are not requiring that )
Then defines a coloring of
with finitely many colors, and Ramsey’s theorem guarantees that there is some
such that
is constant. Let
be the enumeration of
Let and let
if
and
then
We claim that is
-canonical on
Step 1: Suppose and
We need to prove that
For this, we define a transformation as follows:
- If
then
- Otherwise, let
be least such that
(so
.) Let
be such that
and
Then, by definition of
and
We then set
Iterating we see that
for some
such that
and we are done.
Step 2: Conversely, suppose that that
and that
We need to prove that
Assume otherwise. Define an equivalence relation on pairs of elements of by setting
for
iff there is an order isomorphism
such that
and
The following is immediate from the fact that is homogeneous for
For let
For
let
be such that
Then there is:
- An
such that
- An
such that
- An
such that
Say that enumerates
Then, by definition of
and recalling that
we have that
Since we can then find
with
such that
for
Let
be such that
Define by setting
and
Note that since then
However, by choice of and the definition of
we have that
and
and therefore (since
is homogeneous for
)
and (by Lemma 12)
contradiction.
It follows immediately that Let
We can then find
and
such that
is
-canonical on
If
then
is constant. For
by passing to an appropriate proper subset of
we necessarily make the range of
smaller. In either case, we find an infinite subset
of
such that
We can extract a bit of additional information from the proof of Theorem 9 without too much effort. I state the result without proof.
Definition 13 Let
and consider a coloring
![{f: [Acup B ]^r rightarrow F.}](https://s0.wp.com/latex.php?latex=%7Bf%3A+%5BAcup+B+%5D%5Er+rightarrow+F.%7D&bg=ffffff&fg=000000&s=0&c=20201002)
Say that
is invariant iff whenever
and
with
as in the proof of Theorem 9 above, then
iff
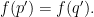
Say that
is isomorphic to

iff whenever
and
is the unique order isomorphism, then
iff
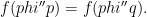
Say that
is stationary iff
for all
![{Bin[A]^omega.}](https://s0.wp.com/latex.php?latex=%7BBin%5BA%5D%5Eomega.%7D&bg=ffffff&fg=000000&s=0&c=20201002)
Then we have:
Theorem 14 (Rado) The following are equivalent for
and
![{f:[A]^rrightarrowomega:}](https://s0.wp.com/latex.php?latex=%7Bf%3A%5BA%5D%5Errightarrowomega%3A%7D&bg=ffffff&fg=000000&s=0&c=20201002)
is invariant.
is stationary.
is
-canonical on
for some

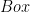
3. Colorings of pairs. II
Magidor has shown that, consistently, every stationary subset of may reflect. Therefore we cannot apply Theorem 5 to conclude that
Fortunately, this case is covered by another result of
Recall from Theorem 20 in lecture II.12 that for every singular cardinal there is an increasing sequence
of regular cardinals cofinal in
such that
i.e., there is a sequence where each
and we have that
whenever
and that for any
there is some
such that
where
iff for all but boundedly many
we have that
We call such a tuple a scale for
Theorem 15 (
) Suppose that
is a singular cardinal and that
is a scale for
such that
for all
Then also
![{lambda^+notrightarrow[lambda^+]^2_{lambda^+}.}](https://s0.wp.com/latex.php?latex=%7Blambda%5E%2Bnotrightarrow%5Blambda%5E%2B%5D%5E2_%7Blambda%5E%2B%7D.%7D&bg=ffffff&fg=000000&s=0&c=20201002)
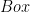
I omit the proof of Theorem 15 (which also uses an elementary substructures argument); see for example the paper by Burke and Magidor cited at the end. Instead, I briefly describe the witnessing coloring:
For each let
witness
Consider the map
where
is the largest
such that
if such
exists, and
otherwise.
Now let be the coloring given by
where
if
and
otherwise.
One then proceeds to show that witnesses
To conclude, the following “stepping up” argument can now be invoked:
Lemma 16 Suppose that
is an infinite cardinal and that
Then also
![{lambda^+notrightarrow[lambda^+]^2_{lambda^+}.}](https://s0.wp.com/latex.php?latex=%7Blambda%5E%2Bnotrightarrow%5Blambda%5E%2B%5D%5E2_%7Blambda%5E%2B%7D.%7D&bg=ffffff&fg=000000&s=0&c=20201002)
Proof: Given witnessing
let
be an injection for all
and set
by
if
and
otherwise.
To see that works, let
and fix
Let
so
but
It follows that there is some
such that
But now we can conclude that there are in
such that
and
Thus
and we are done.
Notice that the result applies to all singular cardinals in a large initial segment of the sequence of cardinals, for example, it applies to all
below the first weakly inaccessible cardinal.
An analysis of the argument showing that indeed works led Shelah to isolate a family of combinatorial principles from which the following result follows:
Theorem 17 (Shelah) If
is singular, then
![{lambda^+notrightarrow[lambda^+]^2_{{rm cf}(lambda)}.}](https://s0.wp.com/latex.php?latex=%7Blambda%5E%2Bnotrightarrow%5Blambda%5E%2B%5D%5E2_%7B%7Brm+cf%7D%28lambda%29%7D.%7D&bg=ffffff&fg=000000&s=0&c=20201002)
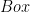
Shelah has also shown that for many inaccessible cardinals (for example, for any cardinal that is inaccessible but not Mahlo.) Further results have been obtained by Eisworth and Shelah.
It is still open whether there can be a successor cardinal (necessarily, the successor of a singular) such that
Before transformed the area with his results, some particular cases were known. The following is from 1965:
Proof: Using that let
enumerate the bounded subsets of
in such a manner that
We claim that there is a function such that for all
in
with
and all
there is
such that
Assume that is such a function, let
and let
Find some
such that
and let
be larger than
and than
Then for some
we have
and we are done.
To prove the claim, for each let
and list
as
Now define
recursively so that
for all
Now set
for all
The following extension of Theorem 18 shows that one can require a stronger property of the witnessing function
Theorem 19 (
-Hajnal-Milner) Assume that
Then there is
such that whenever
are subsets of
with
and
there is
such that

Proof: Let enumerate all partial functions
with
and
Given let
and fix a bijection
where
Now, by transfinite recursion, define so that
for all Notice that this is possible, since
for all
To define we set
for all
and all
and let
for all
not specified by this rule.
We claim that is as wanted. Suppose otherwise, and pick counterexamples
with
and
Define
by picking
for all
Let be such that
and pick
such that
and
Let
for the unique ordinal
such that
Then, by construction,
But this contradicts the definition of
and we are done.
One sometimes writes for
and
and
and
for
and
and
The conclusion of the theorem above can then be stated as saying that
or even that
for all suitable
Corollary 20 Assume
and let
be an outer model with the same reals. Then there is in
a sequence
of pairwise disjoint stationary subsets of
all of which remain stationary in

Notice that this is obvious if we just require that there is some pairwise disjoint collection in of size
consisting of stationary subsets of
all of which belong to
This weaker version is an obvious consequence of the existence of
Ulam matrices in
does not require
to hold in
and only needs that
Proof: With defined in
as in Theorem 19 for
note that
also satisfies the conclusion of Theorem 19 in
since any countable partial function from
to itself in
belongs to
Now define for all
We claim that for some
all the sets
are stationary. Clearly, they are disjoint, and the result follows.
To see the claim, assume otherwise. Then for each we can find
and a club
disjoint from
Now set
This is an uncountable (in fact, a club) set, so there is some
such that
In particular, there is some such that
But
and
so
and we are forced to conclude that
contradiction.
It is worth pointing out that original proof of Theorem 4 implies, by a similar argument, the following version of Corollary 20 that does not depend on
Theorem 21 Assume that
is an outer model and that
Then there is in
a sequence
of pairwise disjoint subsets of
all of which are stationary in

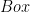
On the other hand, Paul Larson has shown that the conclusion of Corollary 20 (that there is such a sequence of length ) fails in this generality. Larson’s argument builds a forcing extension of
in which reals are added and
is collapsed. It is open whether Corollary 20 holds without the assumption of
but assuming that no reals are added and no cardinals are collapsed.
Note also that the proofs given above of Theorems 4 and 5 do not allow us to conclude Theorem 21, since both constructions depend on a partition into disjoint stationary sets.
In this regard, I should mention here the following recent result of Justin Moore. Moore’s construction allowed him to solve the -space problem and settle several famous problems in set theory and set theoretic topology. Moreover, just as
‘s original proof, Moore’s argument is sufficiently absolute that the function he builds satisfies the conclusion of Theorem 22 in any outer model with the same
Theorem 22 (Moore) There is a function
such that whenever
we have that

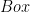
I find it impossible to resist mentioning that Magidor has reproved Corollary 20 with a remarkably short argument. I proceed to include it below; once again, thanks to Assaf Rinot for showing me this result.
Theorem 23 (Magidor) Let
be a cardinal, assume that
and let
be an outer model such that
Then for every stationary
in
that remains stationary in
there exists in
a silly diamond sequence for
over
that is, a sequence
such that, in

is stationary for all

Proof: Working in let
enumerate
Given
let
enumerate
For set
for all It is enough to check that for some
is as wanted.
To see this, assume otherwise. Working in pick
and
for all
so that
for all
Now set
Since
there is some
such that
Let
be larger than
and let
be such that
Then
However,
contradiction.
Corollary 24 Assume
and let
be an outer model with
Then there is in
a partition of
into
stationary sets, all of which remain stationary in

Proof: Note that the assumption guarantees that
Let be a silly diamond sequence for
over
For
let
Then is stationary in
Since
lies in
we are done.
To conclude, I want to mention briefly what the situation is at singular cardinals.
Theorem 25 Let
be a singular cardinal and let
be an integer. Then
![{kappanotrightarrow[kappa]^r_{2^{r-1}}.}](https://s0.wp.com/latex.php?latex=%7Bkappanotrightarrow%5Bkappa%5D%5Er_%7B2%5E%7Br-1%7D%7D.%7D&bg=ffffff&fg=000000&s=0&c=20201002)
Proof: Let be a partition of
into
many sets of size smaller than
Given
let
be the ordinals
such that
and set
Note that the numbers in the sequence are nonzero and add up to
Lemma 26 For any integer
let
be the set of all sequences
where
is an integer, and
and let
Then

Proof: We may as well define noting that
Note also that
For
and
let
be the set of all sequences in
with
Then
and
The result follows now by an obvious induction.
It follows that there are possible values for
and we can then define
by
If there are at least
different ordinals
such that
and it follows that
On the other hand, a version of the Canonization theorem for singular cardinals allows one to show the following:
Theorem 27 Let
be an infinite cardinal such that
Let
be singular strong limit of cofinality
For any integer
and any
we have
i.e., for any coloring
there is an
such that
![{|f''[X]^r|le2^{r-1}.}](https://s0.wp.com/latex.php?latex=%7B%7Cf%27%27%5BX%5D%5Er%7Cle2%5E%7Br-1%7D.%7D&bg=ffffff&fg=000000&s=0&c=20201002)
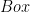
As we will see in future lectures, other than the cardinals
such that
(the weakly compact cardinals) are strongly inaccessible. I suspect that stronger versions of Theorem 27 should be known (with weaker large cardinal restrictions on
or without the strong limit assumption on
), and would be glad to hear of any references.
Bibliography
Here are some references consulted while preparing this note:
- Maxim Burke, Menachem Magidor, Shelah’s pcf theory and its applications, Annals of Pure and Applied Logic, 50 (1990), 207–254.
- Todd Eisworth, Successors of singular cardinals, in Handbook of set theory, Matthew Foreman, Akihiro Kanamori, eds., forthcoming.
- Paul
András Hajnal, Attila Máté, Richard Rado, Combinatorial set theory: partition relations for cardinals, North-Holland (1984).
- Akihiro Kanamori, The higher infinite, Springer (1994).
- Richard Rado, Note on canonical partitions, Bulletin of the London Mathematical Society, 18 (1986), 123-126.
- Assaf Rinot. Surprisingly short, unpublished note; version of April 3, 2009. Available (as of this writing) at his webpage.
- Saharon Shelah, Was Sierpinski right? I, Israel J. Math, 62 (3) (1988), 355–380.
- Stevo
, Walks on ordinals and their characteristics, Birkhäuser (2007).
- Dan Velleman, Partitioning pairs of countable sets of ordinals, The Journal of Symbolic Logic, 55 (3) (Sep., 1990), 1019–1021.
Typeset using LaTeX2WP. Here is a printable version of this post.
Silly fix in the proof of Theorem 18: Rather, let enumerate the subsets of
enumerate the subsets of  of size
of size 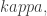 and require that
and require that  for
for 
Ok, I see what the typo is in the proof of Theorem 9 (sorry about the confusion):
In the first paragraph, given of size
of size 
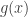 should be the set of all
should be the set of all 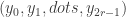 such that:
such that: and
and 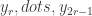 are in
are in ![[2r]^r,](https://s0.wp.com/latex.php?latex=%5B2r%5D%5Er%2C&bg=ffffff&fg=333333&s=0&c=20201002) and
and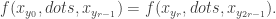
*
*
[…] the Shelah- results from last lecture, we have: Theorem 6 (Shelah, ) If is the successor of a regular cardinal (or simply if is […]
[…] the Shelah- results from last lecture, we have: Theorem 6 (Shelah, ) If is the successor of a regular cardinal (or simply if is […]