502 – König’s lemma | A kind of library

502 – König’s lemma

(The material on mathematical logic is covered in the textbook starting with Chapter 5; however, for the first few lectures, I will be providing some required background topics and will not be following the book. There are several references that you may find useful. For example,

Kaye, Richard. The mathematics of logic, Cambridge University Press (2007).

I am also making use of a set of notes originally developed by Alexander Kechris for the course Math 6c at Caltech.)

1. Notation

We begin by describing some notation and conventions we will need throughout the course.

${{\mathbb N}=\{0,1,\dots\}}$ . In set theory, it is customary to denote ${{\mathbb N}}$ by ${\omega.}$

A sequence is a function whose domain is either ${{\mathbb N}}$ or an initial segment of ${{\mathbb N}}$ (possibly empty).

We identify natural numbers with their set of predecessors. So, if we say, for example, that a sequence has domain ${n\in{\mathbb N}}$ , what we mean is that its domain is ${\{0,1,\dots,n-1\}.}$ If we say that ${i\in k}$ what we mean is that ${i<k}$ .

The length of a sequence is its domain if it is finite, and ${\infty}$ if it is ${{\mathbb N}}$ .

We usually represent sequences as ordered tuples. Thus if ${s}$ is a sequence with domain ${k,}$ we will write

$\displaystyle (s(0),s(1),\dots,s(k-1))$

for ${s}$ . We will usually write ${s_i}$ rather than ${s(i),}$ and omit parentheses and commas if there is no danger of ambiguity, so the sequence above can also be written as

$\displaystyle s_0s_1\dots s_{k-1}.$

The concatenation of two sequences ${s}$ and ${t,}$ where ${s}$ is finite, is the sequence ${s{}^\frown t}$ defined as follows: Let ${n={\rm dom}(s)}$ and ${M={\rm dom}(t)}$ . Then ${s^\frown t}$ is the sequence ${l}$ that has domain ${n+M}$ (if ${M={\mathbb N}}$ then this is just ${{\mathbb N}}$ ) and is given by:

${l(i)=s(i)}$ for ${i<n}$ .
${l(i)=t(i-n)}$ for ${n\le i,}$ ${i\in n+M}$ .

We may write ${st}$ for ${s{}^\frown t}$ and ${si}$ for ${s{}^\frown(i)}$ if ${s}$ and ${t}$ are sequences and ${i}$ is some object.

A tree ${{\mathcal T}}$ is a set of finite sequences with the property that whenever ${s\in{\mathcal T}}$ and ${n<{\rm lh}(s)}$ , then ${s\upharpoonright n \in{\mathcal T}.}$

The typical example of a tree is the (full) binary tree, also called the Cantor tree, ${2^{<{\mathbb N}},}$ consisting of all finite sequences of 0s and 1s.

Trees are partially ordered in a natural way: Given sequences ${s,t,}$ write ${s\sqsubseteq t}$ to indicate that ${s}$ is an initial segment of ${t.}$ The root of a tree is the empty sequence, ${\emptyset,}$ which is an initial segment of any element (node) of the tree. If ${s\sqsubseteq t}$ but ${s\ne t,}$ we write ${s\sqsubset t.}$

Typically, I will imagine trees as growing downward:

If ${s\in{\mathcal T},}$ the successors of ${s}$ are those ${t\in{\mathcal T}}$ such that ${s\sqsubset t.}$ Its predecessors are those ${t}$ such that ${t\sqsubset s;}$ these are just the sequences ${s\upharpoonright n}$ for ${n<{\rm lh}(s).}$ The immediate successors of ${s}$ are the successors of ${s}$ of length ${1+{\rm lh}(s).}$

We can assign a stratification by levels to the tree ${{\mathcal T}}$ in a natural way; namely, the nodes of tree of length ${n}$ form the ${n}$ -th level of ${{\mathcal T}.}$ An infinite branch through a tree ${{\mathcal T}}$ is an infinite sequence ${s}$ such that for all ${n,}$ ${s\upharpoonright n\in{\mathcal T}.}$ Intuitively, branches are paths through ${{\mathcal T}.}$ We denote by ${[{\mathcal T}]}$ the set of all infinite branches through ${{\mathcal T}.}$ Thus

$\displaystyle [2^{<{\mathbb N}}]=2^{\mathbb N}$

is the set of all infinite sequences of 0s and 1s. This is usually called the Cantor set, since it can be naturally identified with Cantor’s ternary subset of ${[0,1].}$ In fact, this identification is a homeomorphism, when we give ${\{0,1\}}$ the discrete topology and ${\{0,1\}^{\mathbb N}}$ the product topology. Recall that in this topology a basic open set is one of the form

$\displaystyle N_s=\{x\in 2^{\mathbb N}\mid s\sqsubset x\}$

for ${s\in 2^{<{\mathbb N}}.}$

2. König’s lemma

A tree is infinite iff it has infinitely many nodes. It is finite branching iff each node has only finitely many immediate successors.

König’s lemma is a very powerful tool that allows us to relate infinite and finite combinatorics, and we will use it frequently throughout the course. Its proof is remarkably simple.

Lemma 1 Let ${{\mathcal T}}$ be an infinite, finite branching tree. Then ${[{\mathcal T}]\ne\emptyset.}$

Proof: By induction, we will identify for each ${n\in{\mathbb N}}$ a node ${s_n}$ in level ${n}$ of ${{\mathcal T}}$ in such a way that

${n<m}$ implies that ${s_n\sqsubset s_m}$ , and
The set of successors of ${s_n}$ is infinite.

Condition (1) above allows us to form the infinite sequence

$\displaystyle s=\bigcup_n s_n.$

By construction, ${s\in[{\mathcal T}],}$ and this will give us the result we want. Condition (2) is used to ensure that we can keep the induction going.

At stage 0 we simply set ${s_0=\emptyset.}$ By hypothesis, ${{\mathcal T}}$ is infinite, so condition (2) is satisfied.

Suppose ${s_n}$ has been defined. Let ${t^0,\dots,t^k}$ list all the immediate successors of ${s_n.}$ There are finitely many of them since ${{\mathcal T}}$ is finite branching. Note also that a successor of ${s_n}$ is either a ${t^i}$ or a successor of ${t^i.}$ It follows that for some ${i\le k,}$ ${t^i}$ has infinitely many successors. Let such ${t^i}$ be ${s_{n+1}.}$ This completes the induction. $\Box$

Exercise 1 Show that König’s lemma is false if we omit the assumption that ${{\mathcal T}}$ is finite branching, even if we require that all levels of ${{\mathcal T}}$ be nonempty.

Here is an application: Define a domino system to be a finite set ${D}$ of domino types, i.e., unit squares (parallel to the axes) whose sides have been labeled. Note that we require that ${D}$ is finite as part of the definition.

For example, ${D}$ could consist of the following domino types:

A tiling by ${D}$ of the plane, or of a finite or infinite subset ${S}$ of the plane, consist of a filling-in of the set ${S}$ by dominoes of type in ${D}$ so that adjacent dominoes have matching labels (no rotations are allowed).

For example, the set ${D}$ above can tile the plane by periodically repeating the pattern below:

Theorem 2 For any domino system ${D,}$ the following are equivalent:

${D}$ can tile the plane.

${D}$ can tile the upper right quadrant.

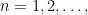
For each ${n=1,2,\dots,}$ ${D}$ can tile the ${n\times n}$ square.

Proof: Clearly, (1) implies (2), and (2) implies (3).

We prove that (3) implies (1). Consider a system ${D}$ that can tile all finite squares. Define a tree ${{\mathcal T}}$ as follows: At level ${0}$ we have the empty sequence. At level ${n>0,}$ we have all tilings ${D}$ of the ${(2n-1)\times(2n-1)}$ square. Such a tiling is an immediate successor of a tiling of the ${(2n-3)\times(2n-3)}$ square iff this smaller tiling occupies the center of the larger one.

(It is straightforward to transform this labeling of nodes into a tree according to our conventions.)

Note that ${{\mathcal T}}$ is infinite (by assumption (3)) and finite branching (since ${D}$ is finite). By König’s lemma, ${[{\mathcal T}]\ne\emptyset,}$ i.e., we can tile the odd-length squares in such a way that we can keep extending the tiling, thus covering the whole plane. This completes the proof. $\Box$

The above is a typical application of König’s lemma. It allows us to replace an infinite problem (tiling the plane) with a series of finite, in principle, more approachable, problems. Other applications do the opposite: They allow us to extract information about finite combinatorics from result about infinite objects. We will see a few more examples next time, and throughout the course.

Typeset using LaTeX2WP. Here is a printable version of this post.

This entry was posted on Monday, August 24th, 2009 at 2:47 pm and is filed under 502: Logic and set theory. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

One Response to 502 – König’s lemma

305 – Friedman’s theorem « Teaching blog says:

February 4, 2012 at 5:11 pm

[…] Part I. […]

Reply

	ปั่นสล็อต on 414/514 The theorems of Rieman…
	Richard Kimberly Hec… on Woodin’s proof of the se…
	Is there a Borel-mea… on 414/514 Examples of Baire clas…
	Simple bijectiveness… on 580 -Some choiceless results…
	Schur’s theore… on 580 -III. Partition calcu…
	Uncountable linearly… on 403/503 – Homework …
	What is a non-constr… on On strong measure zero se…
	function from Nmathb… on Hindsight
	Cauchy Schwarz Inequ… on 275 -Positive polynomials
	What is a Cantor-sty… on 580 -Some choiceless results…
	Question about Gener… on 580 -Some choiceless results…
	Set has Measure Zero… on On strong measure zero se…
	Non-measurable subse… on 580 -Cardinal arithmetic …
	hmeng1 on 414/514 The theorems of Rieman…
	580 -Cardinal arithm… on 580 -Cardinal arithmetic …

M	T	W	T	F	S	S
					1	2
3	4	5	6	7	8	9
10	11	12	13	14	15	16
17	18	19	20	21	22	23
24	25	26	27	28	29	30
31

A kind of library