580 -Cardinal arithmetic (7)

[This document was typeset using Luca Trevisan‘s LaTeX2WP. I will refer to result $n$ (or definition $n$ ) from last lecture as $3.n.$ ]

A. The Galvin-Hajnal rank and an improvement of Theorem 3.1

Last lecture, I covered the first theorem of the Galvin-Hajnal paper and several corollaries. Recall that the result, Theorem 3.1, states that if ${\kappa}$ and ${\lambda}$ are uncountable regular cardinals, and ${\lambda}$ is ${\kappa}$ -inaccessible, then ${\prod_{\alpha<\kappa}\kappa_\alpha<\aleph_\lambda}$ for any sequence ${(\kappa_\alpha:\alpha<\lambda)}$ of cardinals such that ${\prod_{\alpha<\beta}\kappa_\alpha<\aleph_\lambda}$ for all ${\beta<\kappa.}$

In particular (see, for example, Corollary 3.7), if ${{\rm cf}(\xi)>\omega}$ and ${\aleph_\xi}$ is strong limit, then ${2^{\aleph_\xi}<\aleph_{(|\xi|^{{\rm cf}(\xi)})^+}.}$

The argument relied in the notion of an almost disjoint transversal. Assume that ${\kappa}$ is regular and uncountable, and recall that if ${{\mathcal A}=(A_\alpha:\alpha<\kappa)}$ is a sequence of sets, then ${T({\mathcal A})=\sup\{|{\mathcal F}|:{\mathcal F}}$ is an a.d.t. for ${{\mathcal A}\}.}$ Here, ${{\mathcal F}}$ is an a.d.t. for ${{\mathcal A}}$ iff ${{\mathcal F}\subseteq\prod{\mathcal A}:=\prod_{\alpha<\kappa}A_\alpha}$ and whenever ${f\ne g\in{\mathcal F},}$ then ${\{\alpha<\kappa:f(\alpha)=g(\alpha)\}}$ is bounded.

With ${\kappa,\lambda}$ as above, Theorem 3.1 was proved by showing that there is an a.d.t. for ${(\prod_{\beta<\alpha}\kappa_\beta:\alpha<\kappa)}$ of size ${\prod_{\alpha<\kappa}\kappa_\alpha,}$ and then proving that, provided that ${|A_\alpha|<\aleph_\lambda}$ for all ${\alpha<\kappa,}$ then ${T({\mathcal A})<\aleph_\lambda.}$

In fact, the argument showed a bit more. Recall that if ${f:\kappa\rightarrow{\sf ORD},}$ then ${\aleph_f=(\aleph_{f(\alpha)}:\alpha<\kappa).}$ Then, for any ${f:\kappa\rightarrow\lambda}$ , ${T(\aleph_f)<\aleph_\lambda.}$

The proof of this result was inductive, taking advantage of the well-foundedness of the partial order ${<_{b,\kappa}}$ defined on ${{}^\kappa{\sf ORD}}$ by ${f<_{b,\kappa}g}$ iff ${\{\alpha:f(\alpha)\ge g(\alpha)\}}$ is bounded in ${\kappa.}$ That ${<_{b,\kappa}}$ is well-founded allows us to define a rank ${|f|_b}$ for each ${f:\kappa\rightarrow{\sf ORD},}$ and we can argue by considering a counterexample of least possible rank to the statement from the previous paragraph.

In fact, more precise results are possible. Galvin and Hajnal observed that replacing the ideal of bounded sets with the nonstationary ideal (or, really, any normal ideal), results in a quantitative improvement of Theorem 3.1.

Definition 1 For ${f,g:\kappa\rightarrow{\sf ORD},}$ let ${f<_{{\rm NS}_\kappa}g}$ iff ${\{\alpha<\kappa: f(\alpha)\ge g(\alpha)\}}$ is nonstationary. Similarly, define ${f\le_{{\rm NS}_\kappa}g}$ iff ${\{\alpha:f(\alpha)>g(\alpha)\}}$ is nonstationary, etc.

Since ${{\rm NS}_\kappa,}$ the collection of nonstationary subsets of ${\kappa}$ is a ${\kappa}$ -complete (in fact, normal) ideal, then ${<_{{\rm NS}_\kappa}}$ is well-founded, and ${|f|=|f|_{{\rm NS}_\kappa}}$ is defined for any ${f:\kappa\rightarrow{\sf ORD}.}$ ${|\cdot|}$ is usually called the Galvin-Hajnal rank of ${f.}$

Before stating the result, Theorem 8 below, we prove some preliminary lemmas about the behavior of the Galvin-Hajnal rank.

Definition 2 Let ${\kappa}$ be a regular uncountable cardinal. The canonical functions for ${\kappa}$ are defined inductively: A function ${f:\kappa\rightarrow{\sf ORD}}$ is an ${\alpha}$ -th canonical function iff

A ${\beta}$ -th canonical function ${f_\beta:\kappa\rightarrow{\sf ORD}}$ exists for all ${\beta<\alpha,}$

For all ${\beta<\alpha,}$ there is a ${\beta}$ -th canonical function ${f_\beta}$ for ${\kappa}$ such that ${f_\beta<_{{\rm NS}_\kappa}f,}$ and

For all ${h:\kappa\rightarrow{\sf ORD},}$ if for all ${\beta<\alpha}$ there is some ${\beta}$ -th canonical function ${f_\beta}$ for ${\kappa}$ such that ${f_\beta<_{{\rm NS}_\kappa}h,}$ then ${f\le_{{\rm NS}_\kappa}h.}$

Of course, the idea is that an ${\alpha}$ -th canonical function ${f}$ witnesses ${|f|=\alpha}$ and is canonical just as ordinals are canonical among well-ordered sets. We prove this in a series of lemmas.

Lemma 3 If ${\kappa}$ is regular and uncountable, and ${f,g}$ are ${\alpha}$ -th canonical functions for ${\kappa,}$ then ${f=_{{\rm NS}_\kappa}g.}$

Proof: By definition, if ${f}$ and ${g}$ are ${\alpha}$ -th canonical functions for ${\kappa,}$ then both ${f\le_{{\rm NS}_\kappa}g}$ and ${g\le_{{\rm NS}_\kappa}f}$ hold, so ${f=_{{\rm NS}_\kappa}g.}$ $\Box$

By the lemma, we can simply talk about the ${\alpha}$ -th canonical function, if one exists.

Lemma 4 Let ${\kappa}$ be an uncountable regular cardinal, let ${f:\kappa\rightarrow{\sf ORD},}$ and let ${\alpha}$ be such that the ${\alpha}$ -th canonical function ${f_\alpha}$ exists. Then ${|f|>\alpha}$ iff ${f_\alpha<_{{\rm NS}_\kappa}f.}$

Proof: By induction, ${|f_\alpha|\ge\alpha,}$ so if ${f_\alpha<_{{\rm NS}_\kappa}f}$ then ${\alpha<|f|.}$

To prove the other implication, argue by induction, and assume that for all ${\beta<\alpha}$ and all ${g:\kappa\rightarrow{\sf ORD},}$ if ${|g|>\beta}$ then ${f_\beta<_{{\rm NS}_\kappa}g}$ where ${f_\beta}$ is the ${\beta}$ -th canonical function.

Suppose that ${|f|>\alpha.}$ Then there is some ${f'<_{{\rm NS}_\kappa}f}$ such that ${|f'|\ge\alpha.}$ It follows that for any ${\beta<\alpha,}$ ${|f'|>\beta.}$ By induction, ${f_\beta<_{{\rm NS}_\kappa}f'.}$ By definition, ${f_\alpha\le_{{\rm NS}_\kappa}f'.}$ But then ${f_\alpha<_{{\rm NS}_\kappa}f}$ as wanted. $\Box$

Corollary 5 For any regular uncountable cardinal ${\kappa,}$ if the ${\alpha}$ -th canonical function ${f_\alpha}$ for ${\kappa}$ exists, then ${|f_\alpha|=\alpha.}$

Proof: By induction on ${\alpha,}$ ${|f_\alpha|\ge\alpha.}$ But ${|f_\alpha|>\alpha}$ is impossible by Lemma 4. $\Box$

It is easy to exhibit the first few canonical functions.

Lemma 6 Let ${\kappa}$ be a regular uncountable cardinal.

The ${\alpha}$ -th canonical function ${f_\alpha}$ exists for all ${\alpha<\kappa^+.}$

If ${\beta<\kappa}$ then ${|f|\le\beta}$ iff ${\{\alpha:f(\alpha)\le\beta\}}$ is stationary.

${|f|\le\kappa}$ iff ${\{\alpha:f(\alpha)\le\alpha\}}$ is stationary.

Proof: For ${\alpha<\kappa}$ we can set ${f_\alpha}$ to be the function constantly equal to ${\alpha,}$ and we can also set ${f_\kappa}$ to be the identity. It is straightforward from induction and Fodor’s lemma that Definition 2 is satisfied. Items 2 and 3 follow now from Lemma 4.

In general, given ${\kappa<\alpha<\kappa^+,}$ choose a (nonstrictly) increasing sequence of ordinals ${(i_\xi:\xi<\kappa)}$ such that ${\alpha=\sup_\xi(i_\xi+1).}$ This is possible, since ${{\rm cf}(\alpha)\le\kappa.}$ Now set ${f_\alpha(\xi)=\sup_{\xi<\alpha}(f_{i_\xi}(\alpha)+1)}$ for all ${\xi<\kappa.}$

We argue by induction that Definition 2 is satisfied. For this, suppose that ${f_\alpha\not\le_{{\rm NS}_\kappa}h.}$ Then ${\{\xi<\kappa:h(\xi)<\sup_{\rho<\xi}(f_{i_\rho}(\xi)+1)\}}$ is stationary. By Fodor’s lemma, there is some fixed ${\rho<\kappa}$ such that ${\{\xi<\kappa:h(\xi)\le f_{i_\rho}(\xi)\}}$ is stationary. But then ${f_{i_\rho}\not<_{{\rm NS}_\kappa}h.}$ $\Box$

For ${\kappa}$ regular uncountable and ${\alpha\ge\kappa^+,}$ it may or may not be the case that the ${\kappa^+}$ -canonical function ${f_{\kappa^+}}$ exists.

For example, Galvin showed that the ${\omega_2}$ -th function ${f:\omega_1\rightarrow\omega_1}$ does not exist in ${L,}$ while in a model of Jech, Magidor, Mitchell, and Prikry, the ${\alpha}$ -th canonical function ${f:\omega_1\rightarrow\omega_1}$ exists for all ${\alpha.}$ This statement is equiconsistent with the existence of a measurable cardinal (the model is obtained by a construction that gives that ${{\rm NS}_{\omega_1}}$ is precipitous, and it is easy to see that the existence of ${f_\alpha}$ for all ${\alpha}$ implies this). See Thomas Jech, Menachem Magidor, William Mitchell, and Karel Prikry, Precipitous Ideals, The Journal of Symbolic Logic, 45 (1) (Mar., 1980), 1–8.

If one is only interested in the existence of the ${\alpha}$ -th canonical function for ${\omega_1}$ for all ${\alpha<\theta}$ for some fixed ${\theta,}$ this does not require any large cardinals, and its consistency was established in Thomas Jech, Saharon Shelah, A note on canonical functions, Israel J. Math. 68 (3) (1989), 376–380.

Given an uncountable regular cardinal ${\kappa,}$ forcing allows us to specify in which sense the canonical functions for ${\kappa}$ are, indeed, canonical: These are the functions ${f:\kappa\rightarrow{\sf ORD}}$ such that the ordinal ${[f]_G}$ in the internal ultrapower ${V^\kappa/G}$ is independent of the ${{\rm NS}_\kappa}$ -generic filter ${G.}$ This characterization is often taken in place of Definition 2.

Lemma 7 Let ${\kappa}$ be an uncountable regular cardinal and let ${f:\kappa\rightarrow{\sf ORD}.}$

$|f|<\left(\prod_{f(\alpha)\ne0}|f(\alpha)|\right)^+.$

If ${\lambda}$ is regular uncountable and ${\kappa}$ -inaccessible, and ${f:\kappa\rightarrow\lambda,}$ then ${|f|<\lambda.}$

Proof: Suppose ${g<_{{\rm NS}_\kappa}f.}$ Let

$g'(\alpha)=g(\alpha)$ if $g(\alpha)<f(\alpha),$ and $g'(\alpha)=0$ otherwise.

Then ${g'=_{{\rm NS}_\kappa}g}$ so ${|g'|=|g|,}$ ${g'(\alpha)=0}$ if ${f(\alpha)=0,}$ and if ${X=\{\alpha<\kappa: f(\alpha)\ne0\},}$ then the restriction of ${g'}$ to ${X}$ is in the set product ${\prod_{\alpha\in X}f(\alpha).}$ There are at most ${\prod_{\alpha\in X}|f(\alpha)|}$ many such functions ${g',}$ and since any ordinal below ${|f|}$ is represented by one of them, it follows that $|f|<\left(\prod_{f(\alpha)\ne0}|f(\alpha)|\right)^+,$ as wanted.

Item 2 follows immediately, since if ${f:\kappa\rightarrow\lambda}$ then ${f(\alpha)<\lambda}$ for all ${\alpha,}$ and ${\delta=\sup_\alpha f(\alpha)<\lambda,}$ by regularity. But then ${|f|<(\delta^\kappa)^+\le\lambda.}$ $\Box$

Shelah has shown (by a more elaborate argument) that Lemma 7.2 still holds if one weakens the ${\kappa}$ -inaccessibility assumption on ${\lambda}$ to the requirement that ${\tau^\kappa<\lambda}$ for all ${\tau<\lambda}$ of cofinality ${\kappa.}$ This allows us to weaken the assumption in the same way in the corollaries below.

We are now ready to state the second Galvin-Hajnal theorem.

For notational convenience, let’s write ${T(\kappa,\delta)}$ for ${T({\mathcal A})}$ where ${{\mathcal A}=(A_\alpha:\alpha<\kappa)}$ with ${A_\alpha=\delta}$ for all ${\alpha<\kappa.}$

Theorem 8 (Galvin-Hajnal) Let ${\kappa}$ be an uncountable regular cardinal, let ${(\delta_\alpha:\alpha<\kappa)}$ be a (not necessarily strictly) increasing continuous sequence of cardinals, let ${\varphi:\kappa\rightarrow{\sf ORD}}$ and set ${\psi(\alpha)=\delta_\alpha^{+\varphi(\alpha)}}$ for ${\alpha<\kappa.}$ If ${\Delta=2^\kappa\sup_{\alpha<\kappa}T(\kappa,\delta_\alpha),}$ then ${T(\psi)\le\Delta^{+|\varphi|}.}$

The proof of Theorem 8 is by induction on ${|\varphi|.}$ When the ${\delta_\alpha}$ are strictly increasing and ${|\varphi|=0,}$ this is a result of Erdős, Hajnal, and Milner.

Corollary 9 If ${\kappa}$ is uncountable regular and ${\varphi:\kappa\rightarrow{\sf ORD},}$ then ${T(\aleph_\varphi)\le(2^\kappa)^{+|\varphi|}.}$

Proof: In the notation of Theorem 8, take ${\delta_\alpha=\omega}$ for all ${\alpha<\kappa,}$ so ${\psi(\alpha)=\aleph_{\varphi(\alpha)}}$ and ${T(\aleph_\varphi)=T(\psi).}$ Note that ${\Delta=2^\kappa T(\kappa,\omega)=2^\kappa.}$ $\Box$

Notice that Theorem 3.1 follows immediately:

Corollary 10 Suppose that ${\kappa,\lambda}$ are uncountable regular cardinals and ${\lambda}$ is ${\kappa}$ -inaccessible. If ${f:\kappa\rightarrow\lambda}$ then ${T(\aleph_f)<\aleph_\lambda.}$

Proof: By Corollary 9, ${T(\aleph_f)\le(2^\kappa)^{+|f|}}$ and by Lemma 7, ${|f|<\lambda.}$ $\Box$

Corollary 11 Let ${\kappa,(\delta_\alpha)_{\alpha<\kappa},\Delta,\varphi}$ be as in Theorem 8.

Let ${(\tau_\alpha:\alpha<\kappa)}$ be a sequence of cardinals such that ${\forall\beta<\kappa,\,\prod_{\alpha<\beta}\tau_\alpha\le\delta_\beta^{+\varphi(\beta)}.}$ Then ${\prod_{\alpha<\kappa}\tau_\alpha\le\Delta^{+|\varphi|}.}$

Let ${(\tau_\alpha:\alpha<\kappa)}$ be an increasing sequence of nonzero cardinals such that ${\forall\beta<\kappa,\,\prod_{\alpha<\beta}\tau_\alpha\le\delta_\beta^{+\varphi(\beta)}.}$ Then $\left(\sum_{\alpha<\kappa}\tau_\alpha\right)^\kappa\le\Delta^{+|\varphi|}.$

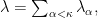
Let ${(\lambda_\alpha:\alpha<\kappa)}$ be a strictly increasing sequence of infinite cardinals. If ${\lambda=\sum_{\alpha<\kappa}\lambda_\alpha,}$ ${\rho}$ is a cardinal, and ${\forall\alpha<\kappa,\,\rho^{\lambda_\alpha}\le\delta_\alpha^{+\varphi(\alpha)},}$ then ${\rho^\lambda\le\Delta^{+|\varphi|}.}$

Proof: For 1, let ${A_\alpha=\prod_{\beta<\alpha}\tau_\beta}$ and let ${{\mathcal F}}$ be an a.d.t. for ${(A_\alpha:\alpha<\kappa)}$ of size ${\prod_{\beta<\kappa}\tau_\beta.}$ By assumption, ${|A_\alpha|\le\delta_\alpha^{+\varphi(\alpha)}}$ for all ${\alpha,}$ so ${|{\mathcal F}|\le T(\psi)\le\Delta^{+|\varphi|}.}$

For 2, recall from Corollary 8 in lecture II.2 that $\left(\sum_{\alpha<\kappa}\tau_\alpha\right)^\kappa\le\Delta^{+|\varphi|}.$

For 3, let ${\tau_\alpha=\rho^{\lambda_\alpha}}$ for ${\alpha<\kappa.}$ Then ${\prod_{\beta<\alpha}\tau_\beta=\rho^{\sum_{\beta<\alpha}\lambda_\beta}\le\rho^{\lambda_\alpha}\le\delta_\alpha^{+\varphi(\alpha)}}$ for all ${\alpha<\kappa,}$ and the result follows from item 1. $\Box$

Corollary 12 Let ${\lambda}$ be a cardinal of uncountable cofinality ${\kappa,}$ and suppose that ${\lambda}$ is ${\kappa}$ -inaccessible. Let ${(\lambda_\alpha:\alpha<\kappa)}$ be a strictly increasing and continuous sequence of infinite cardinals cofinal in ${\lambda.}$ Let ${\varphi:\kappa\rightarrow{\sf ORD}.}$

If ${\forall\alpha<\kappa,\,\prod_{\beta<\alpha}\lambda_\beta\le\lambda_\alpha^{+\varphi(\alpha)},}$ then ${\lambda^\kappa\le\lambda^{+|\varphi|}.}$

If ${\forall\alpha<\kappa,\,2^{\lambda_\alpha}\le\lambda_\alpha^{+\varphi(\alpha)},}$ then ${2^\lambda\le\lambda^{+|\varphi|}.}$

If ${2^\tau\le\lambda^\kappa}$ for all ${\tau<\lambda}$ and ${\prod_{\beta<\alpha}\lambda_\beta\le\lambda_\alpha^{+\varphi(\alpha)}}$ for all ${\alpha<\kappa,}$ then ${2^\lambda\le\lambda^{+|\varphi|}.}$

Proof: In Corollary 11, take ${\delta_\alpha=\tau_\alpha=\lambda_\alpha}$ and ${\rho=2.}$ To prove 1, notice that ${\prod_\alpha\lambda_\alpha=\lambda^\kappa}$ and ${\Delta=2^\kappa\sup_\alpha T(\kappa,\lambda_\alpha)=\sup_\alpha\lambda^\kappa=\lambda.}$ Item 2 follows from Corollary 11.3, and item 3 follows from the fact that ${2^\lambda=\lambda^\kappa.}$ $\Box$

Recall the very general statement of Silver’s theorem, Theorem 21 in lecture II.5:

Corollary 13 (Silver) Let ${\lambda}$ be a ${\kappa}$ -inaccessible cardinal of uncountable cofinality ${\kappa.}$ Let ${(\lambda_\alpha:\alpha<\kappa)}$ be a strictly increasing sequence of cardinals cofinal in ${\lambda.}$ Suppose that there is some ${\mu<\kappa}$ such that ${\{\alpha<\kappa: \prod_{\beta<\alpha}\lambda_\beta\le\lambda_\alpha^{+\mu}\}}$ is stationary in ${\kappa.}$ Then ${\lambda^\kappa\le\lambda^{+\mu}.}$

Proof: This follows from Corollary 12.1 and Lemma 6.2. $\Box$

I won’t include a full proof of Theorem 8 and instead present only a sketch. To prove Theorem 8 two additional ingredients (whose proofs I skip) are needed. One is the Erdős-Rado theorem, that we will prove in Chapter III.

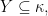
Definition 14 Let ${\kappa,\lambda,\rho}$ be cardinals and let ${n<\omega.}$ Given a set ${X,}$ recall that ${[X]^n=\{Y\subseteq X:|Y|=n\}.}$ The statement ${\kappa\rightarrow(\lambda)^n_\rho}$ means that whenever ${f:[\kappa]^n\rightarrow\rho,}$ there is ${Y\subseteq\kappa,}$ ${|Y|=\lambda,}$ such that the restriction of ${f}$ to ${[Y]^n}$ is constant. If this is not the case, we write ${\kappa\not\rightarrow(\lambda)^n_\rho.}$

It is customary in the field to call the functions ${f}$ as above colorings, and to refer to the sets ${Y}$ as homogeneous with respect to ${f.}$

This “arrow notation” turns to be very useful. For example, the infinitary version of Ramsey’s theorem is simply ${\omega\rightarrow(\omega)^2_2.}$ A well-known example due to Sierpiński shows that ${{\mathfrak c}\not\rightarrow(\omega_1)^2_2}$ or, more generally, ${2^\kappa\not\rightarrow(\kappa^+)^2_2.}$ This will be discussed in Chapter 3.

Theorem 15 (Erdős-Rado) For any infinite cardinal ${\kappa,}$ ${(2^\kappa)^+\rightarrow(\kappa^+)^2_\kappa.}$ ${\Box}$

The second ingredient is a result of Hajnal on set-mappings.

Definition 16 Let ${E}$ be a set. A set-mapping on ${E}$ is a function ${f:E\rightarrow{\mathcal P}(E)}$ such that ${\forall x\in E\,(x\notin f(x))}$ . Given such ${f,E,}$ we say that ${H\subseteq E}$ is free with respect to ${f}$ iff ${\forall x\in H\,(H\cap f(x)=\emptyset).}$

For example, the function ${f:\kappa\rightarrow{\mathcal P}(\kappa)}$ given by ${f(\alpha)=\{\beta<\kappa:\beta\in\alpha\}=\alpha}$ is a set-mapping on ${\kappa,}$ ${|f(\alpha)|<\kappa}$ for all ${\alpha,}$ and any free ${H\subseteq\kappa}$ is a singleton. Ruziewicz conjectured in 1936 that if one strengthens the cardinality restriction on ${f}$ to ${|f(\alpha)|<\lambda}$ for all ${\alpha<\kappa,}$ where ${\lambda<\kappa}$ is some fixed cardinal, then there is now a free ${H}$ of size ${\kappa.}$ This was shown by Hajnal in 1961.

Theorem 17 (Hajnal) Let ${\kappa}$ and ${\lambda}$ be cardinals with ${\lambda<\kappa}$ and ${\kappa}$ infinite. Let ${f}$ be a set-mapping on ${\kappa}$ such that ${|f(\alpha)|<\lambda}$ for all ${\alpha<\kappa.}$ Then there is an ${H\subseteq\kappa}$ of size ${\kappa}$ that is free with respect to ${f.}$ ${\Box}$

Proof of Theorem 8: Proceed by induction on ${|\varphi|.}$

Suppose first that ${|\varphi|=0.}$

Let ${{\mathcal F}}$ be an a.d.t. for ${\psi.}$ By Lemma 6.2, ${\{\alpha<\kappa:\varphi(\alpha)=0\}}$ is stationary. Let ${X_0=\{\alpha:\varphi(\alpha)=0}$ and ${\alpha}$ is limit ${\},}$ so ${X_0}$ is also stationary. Note that ${f(\alpha)<\delta_\alpha}$ for all ${f\in{\mathcal F}}$ and ${\alpha\in X_0}$ and there is therefore a ${\beta_f(\alpha)<\alpha}$ such that ${f(\alpha)<\delta_{\beta_f(\alpha)}.}$ (It is here that the continuity of the sequence ${(\delta_\alpha:\alpha<\kappa)}$ is used.)

By Fodor’s lemma, for each ${f\in{\mathcal F}}$ there is a stationary set ${X_f\subseteq X_0}$ and an ordinal ${\beta_f<\kappa}$ such that ${f(\alpha)<\delta_{\beta_f}}$ for any ${\alpha\in X_f.}$ For fixed sets ${X,\beta,}$ let ${{\mathcal F}_{X,\beta}=\{f\in{\mathcal F}:X_f=X}$ and ${\beta_f=\beta\},}$ and notice that ${{\mathcal F}=\bigcup_{X,\beta}{\mathcal F}_{X,\beta}.}$

Since there are only ${2^\kappa}$ such pairs ${(X,\beta)}$ and ${|{\mathcal F}_{X,\beta}| \le T(\kappa,\delta_\beta)\le\Delta,}$ it follows that ${|{\mathcal F}|\le2^\kappa\Delta=\Delta,}$ and we are done.

Suppose now that ${|\varphi|=\nu>0}$ and that the result holds for all ${\varphi:\kappa\rightarrow{\sf ORD}}$ and corresponding ${\psi}$ such that ${|\varphi|<\nu.}$

Let ${{\mathcal F}}$ be an a.d.t. for ${\psi.}$ For ${f\in{\mathcal F}}$ and ${\alpha<\kappa}$ let ${\varphi_f(\alpha)}$ be least such that ${|f(\alpha)|\le\delta_\alpha^{+\varphi_f(\alpha)},}$ and let ${\psi_f(\alpha)=\delta_{\alpha}^{+\varphi_f(\alpha)}.}$ Notice that ${\varphi_f<_{{\rm NS}_\kappa}\varphi,}$ since ${\varphi_f(\alpha)\ge\varphi(\alpha)}$ only if ${\varphi(\alpha)=0,}$ but the set of these ordinals ${\alpha}$ is nonstationary since ${|\varphi|>0.}$ It follows that ${|\varphi_f|<\nu.}$

This shows that ${{\mathcal F}=\bigcup_{\mu<\nu}{\mathcal F}_\mu,}$ where ${{\mathcal F}_\mu={f\in{\mathcal F}:|\varphi_f|=\mu},}$ and therefore ${|{\mathcal F}|\le|\nu|\sup_{\mu<\nu}|{\mathcal F}_\mu|,}$ and we are done if we show that ${{\mathcal F}_\mu\le\Delta^{+\nu}}$ for each ${\mu<\nu.}$

In fact, ${|{\mathcal F}_\mu|\le\Delta^{+\mu+1}}$ for all ${\mu<\nu.}$ To see this, fix such a ${\mu}$ and begin by defining a set-mapping ${H}$ on ${{\mathcal F}_\mu}$ by

$\displaystyle H(f)=\{g\in{\mathcal F}_\mu:g\ne f\mbox{ and }g\in\prod_{\alpha<\kappa}(f(\alpha)+1)\}.$

Clearly, ${H(f)}$ is an a.d.t. for ${f+1.}$ Note that for all ${\alpha<\kappa,}$ ${|f(\alpha)+1|\le\delta_\alpha^{+\varphi_f(\alpha)}=\psi_f(\alpha),}$ so ${|H(f)|\le T(\psi_f).}$ Notice now that the hypotheses of the theorem apply to ${\varphi_f}$ and ${\psi_f}$ in place of ${\varphi}$ and ${\psi.}$ Since ${|\varphi_f|=\mu<\nu,}$ by the induction hypothesis we have that ${T(\psi_f)\le\Delta^{+\mu}.}$

Let ${\lambda=\Delta^{+\mu+1},}$ and ${\rho=\Delta^{+\mu+2}.}$ If, towards a contradiction, ${|{\mathcal F}_\mu|\ge\rho,}$ then by Theorem 17 there is a set ${{\mathcal F}'\subseteq{\mathcal F}_\mu}$ of size ${\rho}$ that is free with respect to ${H.}$

Notice that ${\rho>\Delta\ge2^\kappa,}$ and therefore (since ${H}$ is free) we can inductively find a sequence ${(f_\xi:\xi<(2^\kappa)^+)}$ with each ${f_\xi\in{\mathcal F}'}$ and ${f_\xi\notin H(f_\eta)}$ whenever ${\xi<\eta<(2^\kappa)^+.}$ By definition of ${H,}$ it follows that for all such ${\xi<\eta}$ there is an ${\alpha=\alpha(\xi,\eta)<\kappa}$ such that ${f_\xi(\alpha)>f_\eta(\alpha).}$

By the Erdős-Rado Theorem 15 there is an infinite set ${A\subseteq (2^\kappa)^+}$ homogeneous for the coloring ${\alpha:[(2^\kappa)^+]^2\rightarrow\kappa.}$ Let ${\gamma<\kappa}$ be the constant value that the map ${\alpha}$ takes on ${[A]^2.}$ If ${\xi<\eta\in A,}$ then ${f_\xi(\gamma)>f_\eta(\gamma),}$ and therefore there is an infinite decreasing sequence of ordinals, contradiction. ${\Box}$

I conclude with an application not mentioned in lecture.

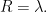
Definition 18 A structure ${{\mathcal M}=(M,R,\dots)}$ in a countable language with a distinguished unary relation (interpreted in ${{\mathcal M}}$ by ${R\subseteq M}$ ) is said to be of type ${(\kappa,\lambda)}$ iff ${|M|=\kappa}$ and ${R=\lambda.}$

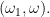
Chang’s conjecture is the statement that whenever ${{\mathcal M}}$ is of type ${(\omega_2,\omega_1),}$ there is an elementary substructure ${{\mathcal N}\prec{\mathcal M}}$ of type ${(\omega_1,\omega).}$

Chang’s conjecture is consistent. It holds under ${{\sf MM}}$ and can be forced from a Ramsey cardinal. A large cardinal of comparable strength is required, since Silver showed that Chang’s conjecture implies the existence of ${0^\sharp.}$

By arguing about Skolem functions, one can show without too much effort that Chang’s conjecture is equivalent to ${\omega_2\rightarrow[\omega_1]^{<\omega}_{\omega_1,\omega},}$ the statement that whenever ${f:[\omega_2]^{<\omega}\rightarrow\omega_1,}$ there is a subset ${A}$ of ${\omega_2}$ of order type ${\omega_1}$ such that ${f''[A]^{<\omega}}$ is countable.

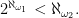
Theorem 19 (Magidor) Chang’s conjecture implies that if ${\aleph_{\omega_1}}$ is strong limit, then ${2^{\aleph_{\omega_1}}<\aleph_{\omega_2}.}$

Notice that from Corollary 3.7 from last lecture without assuming Chang’s conjecture we have that if ${\aleph_{\omega_1}}$ is strong limit then ${2^{\aleph_{\omega_1}}<\aleph_{(2^{\aleph_1})^+}.}$ It is open whether Theorem 19 holds without the additional assumption.

Proof: The following argument is due to Galvin.

By say, Corollary 12, it is enough to show that ${|f|<\omega_2}$ for all ${f:\omega_1\rightarrow\omega_1.}$

To prove this, let ${f:\omega_1\rightarrow{\sf ORD}}$ be such that ${|f|\ge\omega_2.}$ Using Lemma 6, for ${\beta<\omega_2}$ let ${f_\beta}$ be the ${\beta}$ -th canonical function for ${\omega_1,}$ so ${f_\beta<_{{\rm NS}_\kappa}f_\gamma<_{{\rm NS}_\kappa}f}$ for all ${\beta<\gamma<\omega_2.}$ Let ${C_{\beta,\gamma}}$ be a club witnessing this, so for all ${\alpha<\omega_1,}$ if ${\alpha\in C_{\beta,\gamma}}$ then ${f_\beta(\alpha)<f_\gamma(\alpha)<f(\alpha).}$

Define ${h:[\omega_2]^{<\omega}\rightarrow\omega_1}$ as follows: If ${x\subseteq\omega_2}$ is finite, let ${h(x)=\min\bigcap\{C_{\beta,\gamma}:\beta,\gamma\in x,\beta<\gamma\},}$ where we take the minimum of an empty intersection to be zero.

By Chang’s conjecture, there is an ${A\subseteq\omega_2}$ of order type ${\omega_1}$ such that ${\alpha=\sup h''[A]^{<\omega}<\omega_1.}$

We claim that ${f(\alpha)\ge\omega_1,}$ which concludes the proof.

To see the claim, notice first that ${\alpha\in C_{\beta,\gamma}}$ whenever ${\beta,\gamma\in A}$ and ${\beta<\gamma.}$ Suppose otherwise, and fix ${\beta_1<\gamma_1}$ counterexamples. Then ${\alpha_1:=\sup(C_{\beta_1,\gamma_1})\cap(\alpha+1)=\max(C_{\beta_1,\gamma_1})\cap\alpha<\alpha.}$ By definition of ${\alpha,}$ this means that there must be some finite ${x\subset A}$ such that ${h(x)>\alpha_1}$ and therefore, by definition of ${h}$ and ${\alpha_1,}$ it follows that ${h(x\cup\{\beta_1,\gamma_1\})>\alpha,}$ contradiction.

But the claim concludes the proof, since then ${f_\beta(\alpha)<\gamma}$ in ${A,}$ and therefore, since ${|A|=\omega_1,}$ we must have ${f(\alpha)\ge\omega_1.}$ $\Box$

Besides the original Galvin-Hajnal paper, a good reference for this lecture is the book Paul Erdös, András Hajnal, Attila Máté, Richard Rado, Combinatorial set theory: Partition relations for cardinals, North-Holland (1984).

[Here is a printable version of this post.]

This entry was posted on Wednesday, March 4th, 2009 at 12:21 am and is filed under 580: Topics in set theory. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

6 Responses to 580 -Cardinal arithmetic (7)

580 -Cardinal arithmetic (12) « Teaching page says:

March 13, 2009 at 12:23 am

[…] the Galvin-Hajnal results on powers of singulars of uncountable cofinality (see lectures II.6 and II.7). His first success was an extension to cardinals of countable cofinality. For example: Theorem […]

Reply
580 -Partition calculus (2) « Teaching page says:

April 1, 2009 at 10:56 pm

[…] for ordinals. We briefly encountered this weakening when discussing Chang’s conjecture in lecture II.7. Definition 16 Given ordinals say that iff for any there is an such that Similarly, by […]

Reply
hurburble says:

March 15, 2010 at 11:48 am

Hi again,

little typo in the proof of Th 8: In two places it should be $|f(\alpha)|\le\delta_\alpha^{+\varphi_f(\alpha)},$ instead of $|f(\alpha)|\le\delta_\alpha^{\varphi_f(\alpha)},$

Thanks for the notes by the way

Reply
andrescaicedo says:

March 16, 2010 at 10:26 am

Ha! Well spotted, thanks. There was another + missing, $|{\mathcal F}_\mu|\le\Delta^{+\mu+1}.$ (Corrected now, but not in the pdf.)

I am *slowly* turning the notes into a book, and would like to mention you in the acknowledgements section. What name should I use? (If you rather tell me by email, try a_b94@hotmail.com, which is the account I keep for these matters.)

Reply
580 -Partition calculus (2) « A kind of library says:

January 20, 2013 at 9:37 am

[…] We also need the notion of Rowbottom cardinal, that requires a significant weakening of the ordinary partition relation for ordinals. We briefly encountered this weakening when discussing Chang’s conjecture in lecture II.7. […]

Reply
580 -Cardinal arithmetic (12) « A kind of library says:

January 20, 2013 at 9:53 am

[…] the Galvin-Hajnal results on powers of singulars of uncountable cofinality (see lectures II.6 and II.7). His first success was an extension to cardinals of countable cofinality. For […]

Reply

	ปั่นสล็อต on 414/514 The theorems of Rieman…
	Richard Kimberly Hec… on Woodin’s proof of the se…
	Is there a Borel-mea… on 414/514 Examples of Baire clas…
	Simple bijectiveness… on 580 -Some choiceless results…
	Schur’s theore… on 580 -III. Partition calcu…
	Uncountable linearly… on 403/503 – Homework …
	What is a non-constr… on On strong measure zero se…
	function from Nmathb… on Hindsight
	Cauchy Schwarz Inequ… on 275 -Positive polynomials
	What is a Cantor-sty… on 580 -Some choiceless results…
	Question about Gener… on 580 -Some choiceless results…
	Set has Measure Zero… on On strong measure zero se…
	Non-measurable subse… on 580 -Cardinal arithmetic …
	hmeng1 on 414/514 The theorems of Rieman…
	580 -Cardinal arithm… on 580 -Cardinal arithmetic …

A kind of library