414/514 Homework 2 – Monotone and Baire one functions

This set is due in three weeks, on Monday, November 3, at the beginning of lecture.

1. Let $f:[a,b]\to\mathbb R$ be increasing. We know that $f(x-)$ and $f(x+)$ exist for all $x\in[a,b]$ , and that $f$ has at most countably many points of discontinuity, say $t_1,t_2,\dots$ For each $i$ let $I_i,J_i$ be the intervals $(f(t_i-),f(t_i))$ and $(f(t_i),f(t_i+))$ . Some of these intervals may be empty, but for each $i$ at least one of them is not. (Here we follow the convention that $f(a-)=f(a)$ and $f(b+)=f(b)$ .) Let $\mathrm{lh}(I)$ denote the length of the interval $I$ , and say that an interval $(\alpha,\beta)$ precedes a point $t$ iff $\beta\le t$ .

Verify that $\sum_i(\mathrm{lh}(I_i)+\mathrm{lh}(J_i))<+\infty$ and, more generally, for any $x$ ,

$s(x):=\sum\{\mathrm{lh}(I_i)\mid I_i$ precedes $f(x)\}$ $+\sum\{\mathrm{lh}(J_i)\mid J_i$ precedes $f(x)\}<+\infty$ .

Define a function $f_0:[a,b]\to\mathbb R$ by setting $f_0(x)=f(x)-s(x)$ . Show that $f_0$ is increasing and continuous.

Now, for each $n>0$ , define $f_n:[a,b]\to\mathbb R$ so that $f_n\upharpoonright[a,t_n)=f_{n-1}\upharpoonright[a,t_n)$ , $f_n(t_n)=f_{n-1}(t_n)+\mathrm{lh}(I_n)$ , and $f_n(x)=f_{n-1}(x)+\mathrm{lh}(I_n)+\mathrm{lh}(J_n)$ for all $x\in(t_n,b]$ . Show that each $f_n$ is increasing, and its only discontinuity points are $t_1,\dots,t_n$ .

Prove that $f_n\to f$ uniformly.

Use this to provide a (new) proof that increasing functions are in Baire class one.

2. Solve exercise 3.Q in the van Rooij-Schikhof book: If $f:[a,b]\to\mathbb R$ is such that for all $x$ , we have that $f(x-)$ and $f(x+)$ exist, then $f$ is the uniform limit of a sequence of step functions. The approach suggested in the book is the following:

Show that it suffices to argue that for every $\epsilon>0$ there is a step function $s$ such that $|f(x)-s(x)|<\epsilon$ for all $x$ .

To do this, consider the set $A=\{x\in[a,b]\mid$ there is a step function $s$ on $[a,x]$ such that $|f(t)-s(t)|<\epsilon$ for all $t\in[a,x]\}$ .

Show that $A$ is non-empty. Show that if $a\le y\le x$ and $x\in A$ , then also $y\in A$ . This shows that $A$ is an interval ${}[a,\alpha)$ or ${}[a,\alpha]$ , with $\alpha\le b$ . Show that in fact the second possibility occurs, that is, $\alpha\in A$ . For this, the assumption that $f(\alpha-)$ exists is useful. Finally, show that $\alpha=b$ . For this, use now the assumption that $f(\alpha+)$ exists.

3. (This problem is optional.) Find a counterexample to the following statement: If $f:[a,b]\to\mathbb R$ is the pointwise limit of a sequence of functions $f_1,f_2,\dots$ , then there is a dense subset $X\subseteq [a,b]$ where the convergence is in fact uniform. What if $f$ and the functions $f_n$ are continuous? Can you find a (reasonable) weakening of the statement that is true?

4. (This is example 1.1 in Andrew Bruckner’s Differentiation of real functions, CRM monograph series, AMS, 1994. MR1274044 (94m:26001).) We want to define a function $f:[0,1]\to\mathbb R$ . Let $C$ be the Cantor set in ${}[0,1]$ . Whenever $(a,b)$ is one of the components of the complement of $C$ , we define $f(x)=(2(x-a)/(b-a))-1$ for $x\in[a,b]$ . For $x$ not covered by this case, we define $f(x)=0$ . Verify that $f$ is a Darboux continuous function, and that it is discontinuous at every point of $C$ .

Verify that $f$ is not of Baire class one, but that there is a Baire class one function that coincides with $f$ except at (some of) the endpoints of intervals $[a,b]$ as above.

Verify that $f$ is in Baire class two.

This entry was posted on Friday, October 10th, 2014 at 12:45 pm and is filed under 414/514: Analysis I. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

3 Responses to 414/514 Homework 2 – Monotone and Baire one functions

andrescaicedo says:

October 17, 2014 at 10:55 am

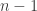I have corrected the definition of the function $s$ in problem 1. Thanks to Jeremy Siegert for noticing the typo in the original version, and for noting that an $n-1$ should be $n$ .

Thanks to Stuart Nygard for noticing a further typo in question 2 (some $x$ should have been $t$ s). Fixed now.

Reply
Jeremy Siegert says:

October 18, 2014 at 2:21 pm

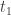In problem 1 we are supposed to show that each $f_{n}$ is discontinuous on the points $t_{1},\dots,t_{n-1}$ . There is no $t_{0}$ based on how we indexed $f$ ‘s points of discontinuity, but it looks as though $f_{1}$ is discontinuous at $t_{1}$ . Should it be that each $f_{n}$ is discontinuous on 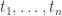$t_{1},\dots,t_{n}$ ?

Reply
- andrescaicedo says:
  
  October 18, 2014 at 10:17 pm
  
  Yes, exactly.
  
  Reply

	ปั่นสล็อต on 414/514 The theorems of Rieman…
	Richard Kimberly Hec… on Woodin’s proof of the se…
	Is there a Borel-mea… on 414/514 Examples of Baire clas…
	Simple bijectiveness… on 580 -Some choiceless results…
	Schur’s theore… on 580 -III. Partition calcu…
	Uncountable linearly… on 403/503 – Homework …
	What is a non-constr… on On strong measure zero se…
	function from Nmathb… on Hindsight
	Cauchy Schwarz Inequ… on 275 -Positive polynomials
	What is a Cantor-sty… on 580 -Some choiceless results…
	Question about Gener… on 580 -Some choiceless results…
	Set has Measure Zero… on On strong measure zero se…
	Non-measurable subse… on 580 -Cardinal arithmetic …
	hmeng1 on 414/514 The theorems of Rieman…
	580 -Cardinal arithm… on 580 -Cardinal arithmetic …

M	T	W	T	F	S	S
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30	31

A kind of library